Toán 11 Bài tập cuối chương III Giải Toán 11 Cánh diều trang 79, 80
Giải Toán 11 Bài tập cuối chương III là tài liệu vô cùng hữu ích giúp các em học sinh lớp 11 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 11 Cánh diều tập 1 trang 79, 80.
Toán 11 Cánh diều tập 1 trang 79, 80 được biên soạn đầy đủ, chi tiết trả lời các câu hỏi từ bài 1 đến 6 chương Giới hạn hàm số liên tục giúp các bạn có thêm nhiều nguồn ôn tập đối chiếu với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết giải Toán 11 tập 1 Bài tập cuối chương IIII Cánh diều, mời các bạn cùng theo dõi tại đây.
Giải Toán 11 Bài tập cuối chương III
Toán lớp 11 Cánh diều tập 1 trang 79, 80
Bài tập 1 trang 79
Cho hàm số y = f(x) xác định trên khoảng (a; b) và x0 ∈ (a; b). Điều kiện cần và đủ để hàm số y = f(x) liên tục tại x0 là:
A. limx→x0+fx=fx0;
B. limx→x0−fx=fx0;
C. limx→x0+fx=limx→x0−fx;
D. limx→x0+fx=limx→x0−fx=fx0.
Gợi ý đáp án
Chọn đáp án D
Bài tập 2 trang 79
Tính các giới hạn sau:
a)  \(\lim \frac{2n^{2}+6n+1}{8n^{2}+5}\);
\(\lim \frac{2n^{2}+6n+1}{8n^{2}+5}\);
b)  \(\lim \frac{4n^{2}-3n+1}{-3n^{3}+6n^{2}-2}\);
\(\lim \frac{4n^{2}-3n+1}{-3n^{3}+6n^{2}-2}\);
c)  \(\lim \frac{\sqrt{4n^{2}-n+3}}{8n-5}\);
\(\lim \frac{\sqrt{4n^{2}-n+3}}{8n-5}\);
d)  \(\lim (4-\frac{2^{n+1}}{3^{n}})\);
\(\lim (4-\frac{2^{n+1}}{3^{n}})\);
e)  \(\lim \frac{4.5^{n}+2^{n+2}}{6.5^{n}}\);
\(\lim \frac{4.5^{n}+2^{n+2}}{6.5^{n}}\);
g)  \(\lim \frac{2+\frac{4}{n^{3}}}{6^{n}}\).
\(\lim \frac{2+\frac{4}{n^{3}}}{6^{n}}\).
Gợi ý đáp án
a)  \(\lim \frac{2n^{2}+6n+1}{8n^{2}+5}=\lim \frac{2+\frac{6}{n}+\frac{1}{n^{2}}}{8+\frac{5}{n^{2}}}=\frac{1}{4}\);
\(\lim \frac{2n^{2}+6n+1}{8n^{2}+5}=\lim \frac{2+\frac{6}{n}+\frac{1}{n^{2}}}{8+\frac{5}{n^{2}}}=\frac{1}{4}\);
b)  \(\lim \frac{4n^{2}-3n+1}{-3n^{3}+6n^{2}-2}=\lim \frac{n^{2}(4-\frac{3}{n}+\frac{1}{n^{2}})}{n^{3}(-3+\frac{6}{n}-\frac{2}{n^{3}})}=\lim\frac{1}{n}.(-\frac{4}{3})=0\);
\(\lim \frac{4n^{2}-3n+1}{-3n^{3}+6n^{2}-2}=\lim \frac{n^{2}(4-\frac{3}{n}+\frac{1}{n^{2}})}{n^{3}(-3+\frac{6}{n}-\frac{2}{n^{3}})}=\lim\frac{1}{n}.(-\frac{4}{3})=0\);
c)  \(\lim \frac{\sqrt{4n^{2}-n+3}}{8n-5}=\lim\frac{\sqrt{4-\frac{1}{n}+\frac{3}{n^{2}}}}{8-\frac{5}{n}}=\frac{1}{4}\);
\(\lim \frac{\sqrt{4n^{2}-n+3}}{8n-5}=\lim\frac{\sqrt{4-\frac{1}{n}+\frac{3}{n^{2}}}}{8-\frac{5}{n}}=\frac{1}{4}\);
d)  \(\lim (4-\frac{2^{n+1}}{3^{n}})=\lim(4-(\frac{2}{3})^{n}.2)=4\);
\(\lim (4-\frac{2^{n+1}}{3^{n}})=\lim(4-(\frac{2}{3})^{n}.2)=4\);
e)  \(\lim \frac{4.5^{n}+2^{n+2}}{6.5^{n}}=\lim (\frac{2}{3}+\frac{2}{3}.(\frac{2}{5})^{n})=\frac{2}{3}\);
\(\lim \frac{4.5^{n}+2^{n+2}}{6.5^{n}}=\lim (\frac{2}{3}+\frac{2}{3}.(\frac{2}{5})^{n})=\frac{2}{3}\);
g)  \(\lim \frac{2+\frac{4}{n^{3}}}{6^{n}}=\frac{2+0}{+\infty}=0\).
\(\lim \frac{2+\frac{4}{n^{3}}}{6^{n}}=\frac{2+0}{+\infty}=0\).
Bài tập 3 trang 79
Tính các giới hạn sau:
a)  \(\lim_{x\rightarrow -3}(4x^{2}-5x+6)\);
\(\lim_{x\rightarrow -3}(4x^{2}-5x+6)\);
b)  \(\lim_{x\rightarrow 2}\frac{2x^{2}-5x+2}{x-2}\);
\(\lim_{x\rightarrow 2}\frac{2x^{2}-5x+2}{x-2}\);
c)  \(\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{x^{2}-16}\).
\(\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{x^{2}-16}\).
Gợi ý đáp án
a)  \(\lim_{x\rightarrow -3}(4x^{2}-5x+6)=57\);
\(\lim_{x\rightarrow -3}(4x^{2}-5x+6)=57\);
b)  \(\lim_{x\rightarrow 2}\frac{2x^{2}-5x+2}{x-2}=\lim_{x\rightarrow 2}\frac{(x-2)(x-\frac{1}{2})}{x-2}=2-\frac{1}{2}=\frac{3}{2}\);
\(\lim_{x\rightarrow 2}\frac{2x^{2}-5x+2}{x-2}=\lim_{x\rightarrow 2}\frac{(x-2)(x-\frac{1}{2})}{x-2}=2-\frac{1}{2}=\frac{3}{2}\);
c)  \(\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{x^{2}-16}=\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)}=\lim\frac{1}{(\sqrt{x}+2)(x+4)}=\frac{1}{32}\)
\(\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{x^{2}-16}=\lim_{x\rightarrow 4}\frac{\sqrt{x}-2}{(\sqrt{x}-2)(\sqrt{x}+2)(x+4)}=\lim\frac{1}{(\sqrt{x}+2)(x+4)}=\frac{1}{32}\)
Bài tập 4 trang 79
Tính các giới hạn sau:
a)  \(\lim_{x\rightarrow -\infty}\frac{6x+8}{5x-2}\);
\(\lim_{x\rightarrow -\infty}\frac{6x+8}{5x-2}\);
b)  \(\lim_{x\rightarrow +\infty}\frac{6x+8}{5x-2}\);
\(\lim_{x\rightarrow +\infty}\frac{6x+8}{5x-2}\);
c)  \(\lim_{x\rightarrow -\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}\);
\(\lim_{x\rightarrow -\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}\);
d)  \(\lim_{x\rightarrow +\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}\);
\(\lim_{x\rightarrow +\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}\);
e)  \(\lim_{x\rightarrow -2^{-}}\frac{3x^{2}+4}{2x+4}\);
\(\lim_{x\rightarrow -2^{-}}\frac{3x^{2}+4}{2x+4}\);
g)  \(\lim_{x\rightarrow -2^{+}}\frac{3x^{2}+4}{2x+4}\).
\(\lim_{x\rightarrow -2^{+}}\frac{3x^{2}+4}{2x+4}\).
Gợi ý đáp án
a)  \(\lim_{x\rightarrow -\infty}\frac{6x+8}{5x-2}=\frac{6}{5}\);
\(\lim_{x\rightarrow -\infty}\frac{6x+8}{5x-2}=\frac{6}{5}\);
b)  \(\lim_{x\rightarrow +\infty}\frac{6x+8}{5x-2}=\frac{6}{5}\);
\(\lim_{x\rightarrow +\infty}\frac{6x+8}{5x-2}=\frac{6}{5}\);
c)  \(\lim_{x\rightarrow -\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}=1\);
\(\lim_{x\rightarrow -\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}=1\);
d)  \(\lim_{x\rightarrow +\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}=1\);
\(\lim_{x\rightarrow +\infty}\frac{\sqrt{9x^{2}-x+1}}{3x-2}=1\);
e)  \(\lim_{x\rightarrow -2^{-}}\frac{3x^{2}+4}{2x+4}=-\infty\);
\(\lim_{x\rightarrow -2^{-}}\frac{3x^{2}+4}{2x+4}=-\infty\);
g)  \(\lim_{x\rightarrow -2^{+}}\frac{3x^{2}+4}{2x+4}=+\infty\).
\(\lim_{x\rightarrow -2^{+}}\frac{3x^{2}+4}{2x+4}=+\infty\).
Bài tập 5 trang 79
Cho hàm số 
a) Với  \(a=0, b=1\), xét tính liên tục của hàm số tại
\(a=0, b=1\), xét tính liên tục của hàm số tại  \(x=2\).
\(x=2\).
b) Với giá trị nào của  \(a, b\) thì hàm số liên tục tại
\(a, b\) thì hàm số liên tục tại  \(x=2\)?
\(x=2\)?
c) Với giá trị nào của  \(a, b\) thì hàm số liên tục trên tập xác định?
\(a, b\) thì hàm số liên tục trên tập xác định?
Gợi ý đáp án
a) Ta có: a=0, b=1 thì
Có:  \(f(2)=4\)
\(f(2)=4\)
 \(\lim_{x\rightarrow 2^{-}} f(x)=2.2=4\)
\(\lim_{x\rightarrow 2^{-}} f(x)=2.2=4\)
 \(\lim_{x\rightarrow 2^{+}} f(x)=-3.2+1=-5\)
\(\lim_{x\rightarrow 2^{+}} f(x)=-3.2+1=-5\)
Do đó:  \(\lim_{x\rightarrow 2^{+}} f(x)\neq \lim_{x\rightarrow 2^{-}} f(x)=f(2)\)
\(\lim_{x\rightarrow 2^{+}} f(x)\neq \lim_{x\rightarrow 2^{-}} f(x)=f(2)\)
Vậy hàm số không liên tục tại  \(x=2\).
\(x=2\).
b) Ta có:  \(f(2)=4\)
\(f(2)=4\)
 \(\lim_{x\rightarrow 2^{-}} f(x)=4+a\)
\(\lim_{x\rightarrow 2^{-}} f(x)=4+a\)
 \(\lim_{x\rightarrow 2^{+}} f(x)=-6+b\)
\(\lim_{x\rightarrow 2^{+}} f(x)=-6+b\)
Để hàm số liên tục tại  \(x=2\) thì:
\(x=2\) thì:  \(4+a=-6+b=4\Leftrightarrow a=0; b=10\).
\(4+a=-6+b=4\Leftrightarrow a=0; b=10\).
Vậy  \(a=10; b=0\) thì hàm số liên tục tại
\(a=10; b=0\) thì hàm số liên tục tại  \(x=2\).
\(x=2\).
c) TXĐ:  \(\mathbb{R}\)
\(\mathbb{R}\)
Do  \(f(x)=2x+a\) nếu
\(f(x)=2x+a\) nếu  \(x< 2\) nên hàm số liên tục trên khoảng
\(x< 2\) nên hàm số liên tục trên khoảng  \((-\infty,2)\).
\((-\infty,2)\).
Do  \(f(x)=-3x+b\) nếu
\(f(x)=-3x+b\) nếu  \(x> 2\) nên hàm số liên tục trên khoảng
\(x> 2\) nên hàm số liên tục trên khoảng  \((2,+\infty)\).
\((2,+\infty)\).
Nếu  \(a=0; b=10\) thì hàm số liên tại điểm
\(a=0; b=10\) thì hàm số liên tại điểm  \(x=2\).
\(x=2\).
Do đó khi  \(a=0; b=10\) thì hàm số liên tục trên
\(a=0; b=10\) thì hàm số liên tục trên  \(\mathbb{R}\).
\(\mathbb{R}\).
Bài tập 6 trang 80
Từ độ cao 55, 8 m của tháp nghiêng Pisa nước Ý, người ta thả một quả bóng cao su chạm xuống đất (Hình 18). Giả sử mỗi lần chạm đất quả bóng lại nảy lên độ cao bằng  \(\frac{1}{10}\) độ cao mà quả bóng đạt được trước đó. Gọi
\(\frac{1}{10}\) độ cao mà quả bóng đạt được trước đó. Gọi  \(S_{n}\) là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất
\(S_{n}\) là tổng độ dài quãng đường di chuyển của quả bóng tính từ lúc thả ban đầu cho đến khi quả bóng đó chạm đất  \(n\) lần. Tính
\(n\) lần. Tính  \(\lim S_{n}\).
\(\lim S_{n}\).
Gợi ý đáp án
![S_{n} = \frac{55,8\left [ 1-(1-\frac{1}{10})^{n} \right ]}{1-(1-\frac{1}{10})}=558(1-0,9^{n})](https://st.download.vn/data/image/blank.png) \(S_{n} = \frac{55,8\left [ 1-(1-\frac{1}{10})^{n} \right ]}{1-(1-\frac{1}{10})}=558(1-0,9^{n})\)
\(S_{n} = \frac{55,8\left [ 1-(1-\frac{1}{10})^{n} \right ]}{1-(1-\frac{1}{10})}=558(1-0,9^{n})\)
Suy ra:  \(\lim S_{n}= \lim 558(1-0,9^{n})=558\)
\(\lim S_{n}= \lim 558(1-0,9^{n})=558\)
Bài tập 7 trang 80
Cho một tam giác đều  \(ABC\) cạnh
\(ABC\) cạnh  \(a\). Tam giác
\(a\). Tam giác  \(A_{1}B_{1}C_{1}\) có các đỉnh là trung điểm các cạnh của tam giác
\(A_{1}B_{1}C_{1}\) có các đỉnh là trung điểm các cạnh của tam giác  \(ABC\), tam giác
\(ABC\), tam giác  \(A_{2}B_{2}C_{2}\) có các đỉnh là trung điểm các cạnh của tam giác
\(A_{2}B_{2}C_{2}\) có các đỉnh là trung điểm các cạnh của tam giác  \(A_{1}B_{1}C_{1}\), ..., tam giác
\(A_{1}B_{1}C_{1}\), ..., tam giác  \(A_{n+1}B_{n+1}C_{n+1}\) có các đỉnh là trung điểm các cạnh của tam giác
\(A_{n+1}B_{n+1}C_{n+1}\) có các đỉnh là trung điểm các cạnh của tam giác  \(A_{n}B_{n}C_{n}\), ... Gọi
\(A_{n}B_{n}C_{n}\), ... Gọi  \(p_{1}, p_{2},\) ...,
\(p_{1}, p_{2},\) ...,  \(p_{n}\), ... và
\(p_{n}\), ... và  \(S_{1}, S_{2},\) ...,
\(S_{1}, S_{2},\) ...,  \(S_{n}\), ... theo thứ tự là chu vi và diện tích của các tam giác
\(S_{n}\), ... theo thứ tự là chu vi và diện tích của các tam giác  \(A_{1}B_{1}C_{1}, A_{2}B_{2}C_{2}\), ...,
\(A_{1}B_{1}C_{1}, A_{2}B_{2}C_{2}\), ...,  \(A_{n}B_{n}C_{n}\), ... .
\(A_{n}B_{n}C_{n}\), ... .
a) Tìm giới hạn của các dãy số ( \(p_{n}\)) và (
\(p_{n}\)) và ( \(S_{n}\)).
\(S_{n}\)).
b) Tìm các tổng  \(p_{1}+p_{2}+\)...
\(p_{1}+p_{2}+\)... \(+p_{n}+\)... và
\(+p_{n}+\)... và  \(S_{1}+S_{2}+\)...
\(S_{1}+S_{2}+\)... \(+S_{n}+\)... .
\(+S_{n}+\)... .
Gợi ý đáp án
a) Ta có:  \(p_{1}=\frac{a}{2}+\frac{a}{2}+\frac{a}{2}=\frac{3a}{2}\),
\(p_{1}=\frac{a}{2}+\frac{a}{2}+\frac{a}{2}=\frac{3a}{2}\),  \(p_{2}=\frac{3a}{4}\),
\(p_{2}=\frac{3a}{4}\),  \(p_{n}=\frac{3a}{2^{n}}\)
\(p_{n}=\frac{3a}{2^{n}}\)
Suy ra:  \(\lim p_{n}=\lim 3a.\frac{1}{2^{n}}=0\)
\(\lim p_{n}=\lim 3a.\frac{1}{2^{n}}=0\)
Có:  \(S_{ABC}=\frac{a^{2}\sqrt{3}}{4}\),
\(S_{ABC}=\frac{a^{2}\sqrt{3}}{4}\),  \(S_{A_{1}B_{1}C_{1}}=\frac{S}{4}\),
\(S_{A_{1}B_{1}C_{1}}=\frac{S}{4}\),  \(S_{n}=\frac{a^{2}\sqrt{3}}{4}.(\frac{1}{4})^{n}\)
\(S_{n}=\frac{a^{2}\sqrt{3}}{4}.(\frac{1}{4})^{n}\)
Suy ra:  \(\lim S_{n}=\lim \frac{a^{2}\sqrt{3}}{4}.(\frac{1}{4})^{n}=0\)
\(\lim S_{n}=\lim \frac{a^{2}\sqrt{3}}{4}.(\frac{1}{4})^{n}=0\)
b)  \((p_{n})\) là cấp số nhân lùi vô hạn với công bội
\((p_{n})\) là cấp số nhân lùi vô hạn với công bội  \(q=\frac{1}{2}\), ta có:
\(q=\frac{1}{2}\), ta có:
 \(p_{1}+p_{2}+\)...
\(p_{1}+p_{2}+\)... \(+p_{n}+\)...=
\(+p_{n}+\)...= \(\frac{p_{1}}{1-\frac{1}{2}}=2p_{1}=3a\)
\(\frac{p_{1}}{1-\frac{1}{2}}=2p_{1}=3a\)
(S_{n}) là cấp số nhân lùi vô hạn với công bội  \(q=\frac{1}{4}\)
\(q=\frac{1}{4}\)
 \(S_{1}+S_{2}+\)...
\(S_{1}+S_{2}+\)... \(+S_{n}+\)...=
\(+S_{n}+\)...= \(\frac{S_{1}}{1-\frac{1}{4}}=\frac{4}{3}S_{1}=\frac{S}{3}=\frac{a^{2}\sqrt{3}}{12}\)
\(\frac{S_{1}}{1-\frac{1}{4}}=\frac{4}{3}S_{1}=\frac{S}{3}=\frac{a^{2}\sqrt{3}}{12}\)
Bài tập 8 trang 80
Một thấu kính hội tụ có tiêu cự là  \(f\). Gọi
\(f\). Gọi  \(d\) và
\(d\) và  \(d'\) lần lượt là khoảng cách từ một vật thật
\(d'\) lần lượt là khoảng cách từ một vật thật  \(AB\) và từ ảnh
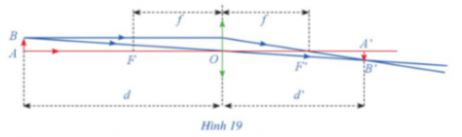
\(AB\) và từ ảnh  \(A'B'\) của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính là
\(A'B'\) của nó tới quang tâm O của thấu kính như Hình 19. Công thức thấu kính là  \(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}\).
\(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f}\).
a) Tìm biểu thức xác đinh hàm số  \(d'=\varphi (d)\).
\(d'=\varphi (d)\).
b) Tìm  \(\lim_{d\rightarrow f^{+}}\varphi (d), \lim_{d\rightarrow f^{-}}\varphi (d), \lim_{d\rightarrow f}\varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.
\(\lim_{d\rightarrow f^{+}}\varphi (d), \lim_{d\rightarrow f^{-}}\varphi (d), \lim_{d\rightarrow f}\varphi (d)\). Giải thích ý nghĩa của các kết quả tìm được.
Gợi ý đáp án
a) Thấu kính hội tụ có tiêu cự f
 \(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f} \Rightarrow \frac{1}{d'}=\frac{1}{f}-\frac{1}{d}=\frac{d-f}{fd}\Rightarrow d'=\frac{fd}{d-f}=\varphi (d)\)
\(\frac{1}{d}+\frac{1}{d'}=\frac{1}{f} \Rightarrow \frac{1}{d'}=\frac{1}{f}-\frac{1}{d}=\frac{d-f}{fd}\Rightarrow d'=\frac{fd}{d-f}=\varphi (d)\)
b) -  \(\lim_{d\rightarrow f^{+}}\varphi (d)=\lim_{d\rightarrow f^{+}}\frac{fd}{d-f}\)
\(\lim_{d\rightarrow f^{+}}\varphi (d)=\lim_{d\rightarrow f^{+}}\frac{fd}{d-f}\)
Ta có:  \(\lim_{d\rightarrow f^{+}}(fd)=f^{2}\);
\(\lim_{d\rightarrow f^{+}}(fd)=f^{2}\);
 \(\lim_{d\rightarrow f^{+}}(d-f)=0\);
\(\lim_{d\rightarrow f^{+}}(d-f)=0\);
 \(d-f> 0\) khi
\(d-f> 0\) khi  \(d\rightarrow f^{+}\).
\(d\rightarrow f^{+}\).
Suy ra:  \(\lim_{d\rightarrow f^{+}}\varphi (d)=+\infty\).
\(\lim_{d\rightarrow f^{+}}\varphi (d)=+\infty\).
Ý nghĩa: Khi đặt vật nằm ngoài tiêu cự và tiến dần đến tiêu điểm thì cho ảnh thật ngược chiều với vật ở vô cùng.
-  \(\lim_{d\rightarrow f^{-}}\varphi (d)=\lim_{d\rightarrow f^{-}}\frac{fd}{d-f}=-\infty\)
\(\lim_{d\rightarrow f^{-}}\varphi (d)=\lim_{d\rightarrow f^{-}}\frac{fd}{d-f}=-\infty\)
Ý nghĩa: Khi đặt vật nằm trong tiêu cự và tiến dần đến tiêu điểm thì cho ảnh ảo cùng chiều với vật và nằm ở vô cùng.
-  \(\lim_{d\rightarrow +\infty}\varphi (d)=\lim_{d\rightarrow +\infty}\frac{fd}{d-f}=\lim_{d\rightarrow +\infty}\frac{f}{1-\frac{f}{d}}=f\)
\(\lim_{d\rightarrow +\infty}\varphi (d)=\lim_{d\rightarrow +\infty}\frac{fd}{d-f}=\lim_{d\rightarrow +\infty}\frac{f}{1-\frac{f}{d}}=f\)
Ý nghĩa: Khi vật được đặt ở xa vô cùng thì sẽ cho ảnh tại tiêu điểm.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-
Văn mẫu lớp 8: Phân tích nhân vật Đôn Ki-hô-tê trong truyện Đánh nhau với cối xay gió
-

Bộ đề thi học kì 2 môn Giáo dục công dân 7 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Bộ đề thi học kì 2 môn Toán 5 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Văn mẫu lớp 7: Đoạn văn cảm nhận tình cảnh của người nông dân trong Sống chết mặc bay
-

Kể lại buổi lễ kỉ niệm ngày Nhà giáo Việt Nam (2 Dàn ý + 10 mẫu)
-

Văn mẫu lớp 8: Cảm nhận về cái kết của truyện Cô bé bán diêm
-

Văn mẫu lớp 12: Phân tích 9 câu đầu bài Đất Nước của Nguyễn Khoa Điềm
-

Bài thu hoạch cá nhân về kết quả học tập, quán triệt Nghị quyết XII
-

Văn mẫu lớp 12: Nghị luận về nỗi sợ hãi của con người (Dàn ý + 8 mẫu)
-

Dàn ý 8 câu đầu bài Tình cảnh lẻ loi của người chinh phụ (5 mẫu)
Mới nhất trong tuần
-
Toán 11 Bài 2: Biến cố hợp và biến cố giao. Biến cố độc lập. Các quy tắc tính xác suất
100+ -
Toán 11 Bài 1: Các số đặc trưng đo xu thế trung tâm cho mẫu số liệu ghép nhóm
100+ -
Toán 11 Bài 1: Góc lượng giác. Giá trị lượng giác của góc lượng giác
1.000+ -
Toán 11 Bài 2: Các quy tắc tính đạo hàm
100+ -

Toán 11 Chủ đề 2: Tính thể tích một số hình khối trong thực tiễn
100+ -

Toán 11 Bài tập cuối chương VIII
100+ -

Toán 11 Bài 6: Hình lăng trụ đứng. Hình chóp đều. Thể tích của một số hình khối
100+ -

Toán 11 Bài 5: Khoảng cách
100+ -

Toán 11 Bài 4: Hai mặt phẳng vuông góc
100+ -

Toán 11 Bài 3: Góc giữa đường thẳng và mặt phẳng. Góc nhị diện
1.000+






 Đề thi học kì 1 Lớp 11
Đề thi học kì 1 Lớp 11
 Đề thi học kì 2 Lớp 11
Đề thi học kì 2 Lớp 11
 Soạn văn 11 Kết nối tri thức
Soạn văn 11 Kết nối tri thức
 Soạn văn 11 Chân trời sáng tạo
Soạn văn 11 Chân trời sáng tạo
 Soạn văn 11 Cánh Diều
Soạn văn 11 Cánh Diều
 Toán 11 Kết nối tri thức
Toán 11 Kết nối tri thức
 Toán 11 Chân trời sáng tạo
Toán 11 Chân trời sáng tạo
 Toán 11 Cánh Diều
Toán 11 Cánh Diều
 Hóa 11 KNTT
Hóa 11 KNTT