Giải Toán 8 Bài 8: Trường hợp đồng dạng của tam giác vuông Giải SGK Toán 8 Hình học Tập 2 (trang 84, 85)
Giải bài tập SGK Toán 8 trang 84, 85 giúp các em học sinh lớp 8 xem gợi ý giải các bài tập của Bài 8: Trường hợp đồng dạng của tam giác vuông Hình học 8 Chương 3. Qua đó các em sẽ nhanh chóng hoàn thiện toàn bộ bài tập của bài 8 Chương III Hình học 8 tập 2.
Giải bài tập Toán Hình 8 tập 2 Bài 8 Chương III: Trường hợp đồng dạng của tam giác vuông
Lý thuyết bài 8: Trường hợp đồng dạng của tam giác vuông
1. Định lí 1
Nếu cạnh huyền và một cạnh góc vuông của tam giác vuông này tỉ lệ với cạnh huyền và một cạnh góc vuông của tam giác vuông kia thì hai tam giác vuông đó đồng dạng.
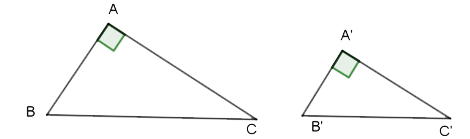
2. Định lí 2
Tỉ số hai đường cao tương ứng của hai tam giác đồng dạng bằng tỉ số đồng dạng.
3. Định lí 3
Tỉ số diện tích của hai tam giác đồng dạng bằng bình phương tỉ số đồng dạng.
Giải bài tập toán 8 trang 84 tập 2
Bài 46 (trang 84 SGK Toán 8 Tập 2)
Trên hình 50 hãy chỉ ra các tam giác đồng dạng. Viết các tam giác này theo thứ tự các đỉnh tương ứng và giải thích vì sao chúng đồng dạng?
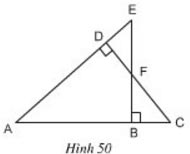
Xét ∆DAC và ∆BAE ta có:
![]() \(\widehat A\) chung
\(\widehat A\) chung
![]() \(\widehat{D} = \widehat{B} = 900\)
\(\widehat{D} = \widehat{B} = 900\)
![]() \(\Rightarrow ∆DAC ∽ ∆BAE\) (g-g)
\(\Rightarrow ∆DAC ∽ ∆BAE\) (g-g)
Xét ∆DFE và ∆BFC có:
![]() \(\widehat{D} = \widehat{B} = 900\)
\(\widehat{D} = \widehat{B} = 900\)
![]() \(\widehat{DFE} = \widehat{BFC}\)(đối đỉnh)
\(\widehat{DFE} = \widehat{BFC}\)(đối đỉnh)
![]() \(\Rightarrow ∆DFE ∽ ∆BFC\) (g-g)
\(\Rightarrow ∆DFE ∽ ∆BFC\) (g-g)
Xét ∆DFE và ∆BAE ta có:
![]() \(\widehat{D} = \widehat{B} = 900\)
\(\widehat{D} = \widehat{B} = 900\)
![]() \(\widehat E\) chung
\(\widehat E\) chung
![]() \(\Rightarrow ∆DFE ∽ ∆BAE\) (g-g)
\(\Rightarrow ∆DFE ∽ ∆BAE\) (g-g)
Do đó: ![]() \(∆DAC ∽ ∆BAE∽ ∆DFE∽ ∆BFC\)
\(∆DAC ∽ ∆BAE∽ ∆DFE∽ ∆BFC\)
Bài 47 (trang 84 SGK Toán 8 Tập 2)
Tam giác ABC có độ dài các cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích là 54cm2. Tính độ dài các cạnh của tam giác A'B'C'.
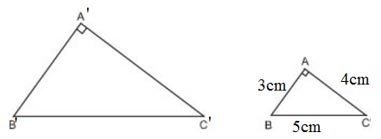
Xét ∆ABC có AB=3cm,AC=4cm,BC=5cm.
Ta có:
![]() \({3^2} + {4^2} = 25 = {5^2} \Rightarrow \Delta ABC\) vuông tại A (định lí Pitago đảo)
\({3^2} + {4^2} = 25 = {5^2} \Rightarrow \Delta ABC\) vuông tại A (định lí Pitago đảo)
Nên ![]() \({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6c{m^2}\)
\({S_{ABC}} = \dfrac{1}{2}AB.AC = \dfrac{1}{2}.3.4 = 6c{m^2}\)
Vì ![]() \(∆ABC ∽ ∆A'B'C'\) (gt)
\(∆ABC ∽ ∆A'B'C'\) (gt)
![]() \(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}}\) (tính chất hai tam giác đồng dạng)
\(\dfrac{{AB}}{{A'B'}} = \dfrac{{BC}}{{B'C'}} = \dfrac{{AC}}{{A'C'}}\) (tính chất hai tam giác đồng dạng)
 \(\Rightarrow \dfrac{S_{ABC}}{S_{A'B'C'}} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\) (tỉ số diện tích bằng bình phương tỉ số đồng dạng)
\(\Rightarrow \dfrac{S_{ABC}}{S_{A'B'C'}} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\) (tỉ số diện tích bằng bình phương tỉ số đồng dạng)
Do đó:  \(\dfrac{6}{54} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\)
\(\dfrac{6}{54} = {\left( {\dfrac{{AB}}{{A'B'}}} \right)^2}\)
 \(\eqalign{
& \Rightarrow {\left( {{{AB} \over {A'B'}}} \right)^2} = {1 \over 9} \cr
& \Rightarrow {{AB} \over {A'B'}} = {1 \over 3} \cr
& \Rightarrow A'B' = 3AB = 3.3 = 9cm \cr}\)
\(\eqalign{
& \Rightarrow {\left( {{{AB} \over {A'B'}}} \right)^2} = {1 \over 9} \cr
& \Rightarrow {{AB} \over {A'B'}} = {1 \over 3} \cr
& \Rightarrow A'B' = 3AB = 3.3 = 9cm \cr}\)
Tức là độ dài mỗi cạnh của tam giác A'B'C' gấp 3 lần độ dài mỗi cạnh của cạnh của tam giác ABC.
Vậy ba cạnh của tam giác A'B'C' là A'B'=9cm, A'C'= 12cm, B'C'=15cm.
Bài 48 (trang 84 SGK Toán 8 Tập 2)
Bóng của cột điện trên mặt đất có độ dài là 4,5m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính chiều cao của cột điện.
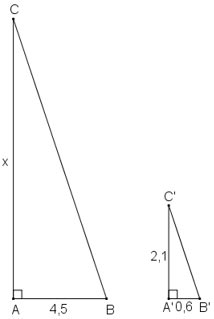
Giả sử cột điện là AB có bóng trên mặt đất là AC.
Thanh sắt là A'B' có bóng trên mặt đất là A'C'.
Vì cột điện và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểm tia sáng tạo với mặt đất một góc bằng nhau nên ta suy ra ![]() \(\widehat {ACB} = \widehat {A'C'B'}\)
\(\widehat {ACB} = \widehat {A'C'B'}\)
![]() \(\Rightarrow\) Hai tam giác vuông ABC và A'B'C' đồng dạng (hai tam giác vuông có hai góc nhọn bằng nhau)
\(\Rightarrow\) Hai tam giác vuông ABC và A'B'C' đồng dạng (hai tam giác vuông có hai góc nhọn bằng nhau)
![]() \(\Rightarrow \dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}\) (tính chất hai tam giác đồng dạng)
\(\Rightarrow \dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}\) (tính chất hai tam giác đồng dạng)
![]() \(\Rightarrow AB = \dfrac{AC.A'B'}{A'C'}\)
\(\Rightarrow AB = \dfrac{AC.A'B'}{A'C'}\)
![]() \(\Rightarrow AB= \dfrac{4,5.2,1}{0,6}= 15,75\, m\)
\(\Rightarrow AB= \dfrac{4,5.2,1}{0,6}= 15,75\, m\)
Vậy cột điện cao 15,75m.
Giải bài tập toán 8 trang 84, 85 tập 2: Luyện tập
Bài 49 (trang 84 SGK Toán 8 Tập 2)
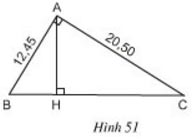
Ở hình 51, tam giác ABC vuông ở A và có đường cao AH.
a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng với nhau? (Hãy chỉ rõ từng cặp tam giác đồng dạng và viết theo các đỉnh tương ứng).
b) Cho biết AB = 12,45cm, AC = 20,50cm. Tính độ dài các đoạn thẳng BC, AH, BH và CH.
![]() \(\widehat{A} = \widehat{H}={90^o}\)
\(\widehat{A} = \widehat{H}={90^o}\)
![]() \(\widehat{B}\) chung
\(\widehat{B}\) chung
![]() \(\Rightarrow ∆ABC ∽ ∆HBA\) (1) (g-g)
\(\Rightarrow ∆ABC ∽ ∆HBA\) (1) (g-g)
Xét ∆ABC và ∆HAC có:
![]() \(\widehat{A} = \widehat{H}={90^o}\)
\(\widehat{A} = \widehat{H}={90^o}\)
![]() \(\widehat{C}\) chung
\(\widehat{C}\) chung
![]() \(\Rightarrow ∆ABC ∽ ∆HAC\) (2) (g-g)
\(\Rightarrow ∆ABC ∽ ∆HAC\) (2) (g-g)
Từ (1) và (2) suy ra ![]() \(∆HAC ∽ ∆HBA\) (vì cùng đồng dạng với ∆ABC)
\(∆HAC ∽ ∆HBA\) (vì cùng đồng dạng với ∆ABC)
b) ∆ABC vuông tại A (giả thiết) nên áp dụng định lí Pitago ta có:
 \(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& \;\;\;\;\;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr
& \Rightarrow BC = \sqrt {575,2525} \approx 24\,cm \cr}\)
\(\eqalign{
& B{C^2} = A{B^2} + A{C^2} \cr
& \;\;\;\;\;\;\;\;= 12,{45^2} + 20,{50^2} = 575,2525 \cr
& \Rightarrow BC = \sqrt {575,2525} \approx 24\,cm \cr}\)
∆ABC ∽ ∆HBA (chứng minh trên)
![]() \(\Rightarrow \dfrac{AB}{HB} = \dfrac{BC}{BA}\)
\(\Rightarrow \dfrac{AB}{HB} = \dfrac{BC}{BA}\)
![]() \(\Rightarrow HB = \dfrac{AB^{2}}{BC} ≈ \dfrac{12,45^{2}}{24}≈ 6,5 cm\)
\(\Rightarrow HB = \dfrac{AB^{2}}{BC} ≈ \dfrac{12,45^{2}}{24}≈ 6,5 cm\)
![]() \(\Rightarrow CH = BC - BH \approx 24 - 6,5 = 17,5 cm.\)
\(\Rightarrow CH = BC - BH \approx 24 - 6,5 = 17,5 cm.\)
Mặt khác: ![]() \(\dfrac{AC}{AH} = \dfrac{BC}{BA}\) (do ∆ABC ∽ ∆HBA theo câu a)
\(\dfrac{AC}{AH} = \dfrac{BC}{BA}\) (do ∆ABC ∽ ∆HBA theo câu a)
![]() \(\Rightarrow AH = \dfrac{AB.AC}{BC} \approx \dfrac{12,45.20,50}{24}\)
\(\Rightarrow AH = \dfrac{AB.AC}{BC} \approx \dfrac{12,45.20,50}{24}\)
![]() \(\Rightarrow AH \approx 10,6 cm\)
\(\Rightarrow AH \approx 10,6 cm\)
Bài 50 (trang 84 SGK Toán 8 Tập 2)
Bóng của một ống khói nhà máy trên mặt đất có độ dài là 36,9m. Cùng thời điểm đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính chiều cao của ống khói (h.52).
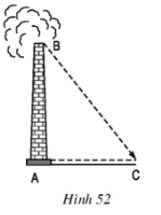
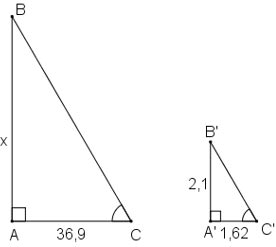
Giả sử thanh sắt là A'B', có bóng là A'C'.
Vì ống khói và thanh sắt đều vuông góc với mặt đất nên hai tam giác ABC và A'B'C' đều là tam giác vuông.
Vì cùng một thời điểm tia sáng chiếu nên ta suy ra ![]() \(\widehat {ACB} = \widehat {A'C'B'}\)
\(\widehat {ACB} = \widehat {A'C'B'}\)
![]() \(\Rightarrow\) Hai tam giác vuông ABC và A'B'C' đồng dạng (hai tam giác vuông có hai góc nhọn bằng nhau)
\(\Rightarrow\) Hai tam giác vuông ABC và A'B'C' đồng dạng (hai tam giác vuông có hai góc nhọn bằng nhau)
![]() \(\Rightarrow \dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}\) (tính chất hai tam giác đồng dạng)
\(\Rightarrow \dfrac{AB}{A'B'} = \dfrac{AC}{A'C'}\) (tính chất hai tam giác đồng dạng)
![]() \(\Rightarrow AB= \dfrac{A'B'.AC}{A'C'}\)
\(\Rightarrow AB= \dfrac{A'B'.AC}{A'C'}\)
![]() \(\Rightarrow AB= \dfrac{2,1.36,9}{1,62}\)
\(\Rightarrow AB= \dfrac{2,1.36,9}{1,62}\)
![]() \(\Rightarrow AB ≈ 47,8m\)
\(\Rightarrow AB ≈ 47,8m\)
Bài 51 (trang 84 SGK Toán 8 Tập 2)
Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn thẳng có độ dài 25cm và 36cm. Tính chu vi và diện tích của tam giác vuông đó (h.53).
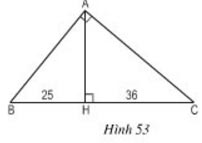
∆AHB ∽ ∆CHA (g.g) vì ![]() \(\widehat{AHB} = \widehat{AHC}=90^o , \widehat{BAH} = \widehat{ACH}\) (cùng phụ với
\(\widehat{AHB} = \widehat{AHC}=90^o , \widehat{BAH} = \widehat{ACH}\) (cùng phụ với ![]() \(\widehat {HAC}\))
\(\widehat {HAC}\))
![]() \(\Rightarrow \dfrac{AH}{CH }= \dfrac{BH}{AH}\)
\(\Rightarrow \dfrac{AH}{CH }= \dfrac{BH}{AH}\)
![]() \(\Rightarrow A{H^2}=CH.BH = 25.36\)
\(\Rightarrow A{H^2}=CH.BH = 25.36\)
![]() \(\Rightarrow A{H^2}= 900 \Rightarrow AH = 30cm\)
\(\Rightarrow A{H^2}= 900 \Rightarrow AH = 30cm\)
Vậy ![]() \(S_{ABC} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.30.(25 + 36) = 915 cm2\)
\(S_{ABC} = \dfrac{1}{2}.AH.BC = \dfrac{1}{2}.30.(25 + 36) = 915 cm2\)
Áp dụng Py-ta-go cho 2 tam giác vuông ABH và ACH ta được:
 \(\begin{array}{l}
A{B^2} = B{H^2} + A{H^2}\\
\Rightarrow A{B^2} = {25^2} + {30^2} = 1525\\ \Rightarrow AB \approx 39,05cm\\
A{C^2} = C{H^2} + A{H^2}\\
\Rightarrow A{C^2} = {36^2} + {30^2} = 2196\\ \Rightarrow AC \approx 46,86cm
\end{array}\)
\(\begin{array}{l}
A{B^2} = B{H^2} + A{H^2}\\
\Rightarrow A{B^2} = {25^2} + {30^2} = 1525\\ \Rightarrow AB \approx 39,05cm\\
A{C^2} = C{H^2} + A{H^2}\\
\Rightarrow A{C^2} = {36^2} + {30^2} = 2196\\ \Rightarrow AC \approx 46,86cm
\end{array}\)
Chu vi tam giác ABC là: P = AB + AC + BC= 39,05 + 46,86 + 61 = 146,91cm
Bài 52 (trang 85 SGK Toán 8 Tập 2)
Cho một tam giác vuông, trong đó cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền.
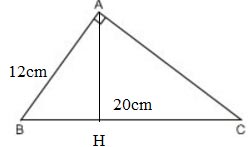
∆ABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC.
Ta có: ∆ABH ∽ ∆CBA vì:
![]() \(\widehat B\) chung
\(\widehat B\) chung
![]() \(\widehat{H} = \widehat{A}=90^o\)
\(\widehat{H} = \widehat{A}=90^o\)
![]() \(\Rightarrow \dfrac{AB}{CB}= \dfrac{BH}{BA}\) (tính chất hai tam giác đồng dạng)
\(\Rightarrow \dfrac{AB}{CB}= \dfrac{BH}{BA}\) (tính chất hai tam giác đồng dạng)
![]() \(\Rightarrow AB^2= HB.CB\)
\(\Rightarrow AB^2= HB.CB\)
![]() \(\Rightarrow BH = \dfrac{AB^{2}}{CB}= \dfrac{12^{2}}{20} = 7,2 \,(cm)\)
\(\Rightarrow BH = \dfrac{AB^{2}}{CB}= \dfrac{12^{2}}{20} = 7,2 \,(cm)\)
![]() \(\Rightarrow CH = BC - BH = 20 - 7,2 = 12,8\,cm\)
\(\Rightarrow CH = BC - BH = 20 - 7,2 = 12,8\,cm\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Bộ đề thi học kì 2 môn Toán 5 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Văn mẫu lớp 7: Đoạn văn cảm nhận tình cảnh của người nông dân trong Sống chết mặc bay
-

Kể lại buổi lễ kỉ niệm ngày Nhà giáo Việt Nam (2 Dàn ý + 10 mẫu)
-

Văn mẫu lớp 8: Cảm nhận về cái kết của truyện Cô bé bán diêm
-

Văn mẫu lớp 12: Phân tích 9 câu đầu bài Đất Nước của Nguyễn Khoa Điềm
-

Bài thu hoạch cá nhân về kết quả học tập, quán triệt Nghị quyết XII
-

Văn mẫu lớp 12: Nghị luận về nỗi sợ hãi của con người (Dàn ý + 8 mẫu)
-

Dàn ý 8 câu đầu bài Tình cảnh lẻ loi của người chinh phụ (5 mẫu)
-

Bộ đề thi học kì 2 môn Khoa học tự nhiên 8 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Văn mẫu lớp 12: Nghị luận về ý kiến Chi tiết nhỏ làm nên nhà văn lớn (Dàn ý + 4 mẫu)
Mới nhất trong tuần
-

Toán 8 Bài 1: Khái niệm hàm số
100+ -

Toán 8 Bài 2: Tọa độ của một điểm và đồ thị của hàm số
100+ -

Toán 8 Bài tập cuối chương III
1.000+ -

Toán 8 Bài 5: Phân thức đại số
1.000+ -

Toán 8 Bài tập cuối chương I
1.000+ -

Toán 8 Bài 2: Các phép toán với đa thức nhiều biến
1.000+ -

Toán 8 Bài 1: Đơn thức và đa thức nhiều biến
1.000+ -
Toán 8 Bài 4: Hệ số góc của đường thẳng
100+ -

Toán 8 Bài 3: Hàm số bậc nhất y = ax + b (a ≠ 0)
100+ 1 -

Toán 8 Bài tập cuối chương 5
1.000+







 Toán 8 Kết nối tri thức
Toán 8 Kết nối tri thức
 Toán 8 Cánh Diều
Toán 8 Cánh Diều
 Toán 8 Chân trời sáng tạo
Toán 8 Chân trời sáng tạo
 Toán 8
Toán 8
 Soạn Văn 8 Kết nối tri thức
Soạn Văn 8 Kết nối tri thức
 Soạn văn 8 Chân trời sáng tạo
Soạn văn 8 Chân trời sáng tạo
 Soạn Văn 8 Cánh Diều
Soạn Văn 8 Cánh Diều
 Chuyên đề Ngữ văn 8
Chuyên đề Ngữ văn 8
 Văn mẫu 8 Kết nối tri thức
Văn mẫu 8 Kết nối tri thức
 Văn mẫu 8 Chân trời sáng tạo
Văn mẫu 8 Chân trời sáng tạo