Toán 8 Luyện tập chung trang 91 Giải Toán 8 Kết nối tri thức tập 2 trang 91, 92

Giải bài tập Toán lớp 8 Luyện tập chung với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa SGK Toán 8 Tập 2 Kết nối tri thức với cuộc sống trang 91, 92. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 8 chi tiết, còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Luyện tập chung Chương IX: Tam giác đồng dạng. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Kết nối tri thức Tập 2 trang 92

Bài 9.11

Cho ΔABC ~ ΔDEF. Biết \(\widehat{A}=60°, \widehat{E}=80°\), hãy tính số đo các góc \(\widehat{B}\), \(\widehat{C}\), \(\widehat{D}\), \(\widehat{F}\)

Lời giải:

Vì ΔABC ~ ΔDEF => \(\widehat{A}=\widehat{D}\), \(\widehat{B}=\widehat{E}\), \(\widehat{C}=\widehat{F}\)

Mà \(\widehat{A}=60°\) => \(\widehat{D}=60°\)

\(\widehat{E}=80°\) => \(\widehat{B}=80°\)

Có \(\widehat{A}+\widehat{B}+\widehat{C}=180°\)

=> \(\widehat{C}=\widehat{F}=180°- 60°- 80°=40°\)

Bài 9.12

Cho ΔABC ~ ΔA'B'C'. Biết \(AB=3cm\), \(A'B'=6cm\) và tam giác ABC có chu vi bằng 10 cm. Hãy tính chu vi tam giác A'B'C'

Lời giải:

Có \(\frac{AB}{A'B'}=\frac{3}{6}=\frac{1}{2}\)

=> ΔABC ~ ΔA'B'C' với tỉ số đồng dạng là \(\frac{1}{2}\)

=> Chu vi tam giác ABC bằng \(\frac{1}{2}\) chu vi tam giác A'B'C'

=> Chu vi A'B'C' là: \(2.10=20\) (cm)

Bài 9.13

Cho hình thang ABCD (AB // CD) có \(\widehat{DAB}=\widehat{DBC}\)

a) Chứng minh rằng ΔABD ~ ΔBDC

b) Giả sử \(AB=2cm, AD=3cm, BD=4cm\). Tính độ dài các cạnh BC và DC

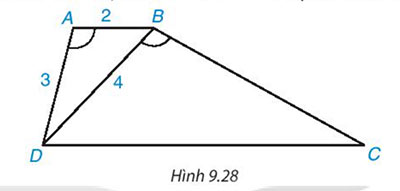
Lời giải:

a) Có AB // CD => \(\widehat{ABD}=\widehat{BDC}\)

- Xét ΔABD và ΔBDC

Có \(\widehat{ABD}=\widehat{BDC}\), \(\widehat{DAB}=\widehat{DBC}\)

=> ΔABD ~ ΔBDC (g.g)

b) Có \(\frac{AB}{BD}=frac{2}{4}=\frac{1}{2}\)

ΔABD ~ ΔBDC với tỉ số \(\frac{1}{2}\)

=> \(\frac{3}{BC}=\frac{4}{DC}=\frac{1}{2}\)

=> \(BC=6\) (cm)

\(DC=8\) (cm)

Bài 9.14

Cho các điểm A, B, C, D, E, F như Hình 9.29. Biết rằng DE // AB, EF // BC, \(DE=4\)cm, \(AB=6\)cm. Chứng minh rằng \(\Delta AEF\) ~ \(\Delta ECD\) và tính tỉ số đồng dạng

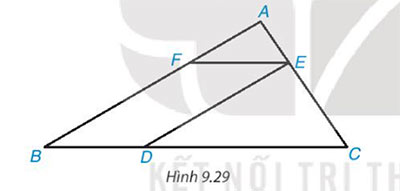
Lời giải:

- Có EF // BC => \(\widehat{AEF}=\widehat{ACD}\) (2 góc đồng vị) (1)

- Có EF // BD (vì EF // BC)

DE // FB (vì MN // BC)

=> EFBD là hình bình hành

=> \(\widehat{EFB}=\widehat{EDB}\)

Mà \(\widehat{EFB}+\widehat{AFE}=180°\)

\(\widehat{EDB}+\widehat{EDC}=180°\)

=> \(\widehat{AFE}=\widehat{EDC}\) (2)

Từ (1) và (2) => ΔAEF ~ ΔECD (g.g)

Có \(\frac{AF}{ED}=\frac{2}{4}=\frac{1}{2}\)

=> Đồng dạng với tỉ số \(\frac{1}{2}\)

Bài 9.15

Cho các điểm A, B, C, D, E như Hình 9.30. Biết rằng \(\widehat{BAC}=\widehat{CDB}\). Chứng minh rằng ΔAED ~ ΔBEC.

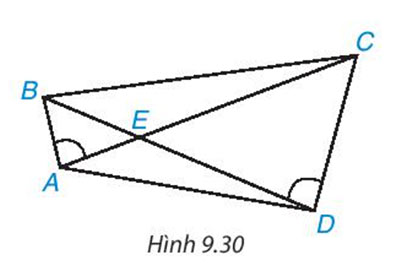
Lời giải:

Xét tam giác AEB và tam giác DEC có:

\(\widehat{BAE} = \widehat{CDE}\) (gt)

\(\widehat{BEA} = \widehat{CED}\) (hai góc đối đỉnh)

Do đó ΔAEB ∽ ΔDEC (g . g)

Suy ra \(\frac{AE}{DE}=\frac{BE}{CE}\) hay \(\frac{AE}{BE}=\frac{DE}{CE}\).

Xét tam giác AED và tam giác BEC có:

\(\frac{AE}{BE}=\frac{DE}{CE}\) (cmt)

\(\widehat{AED} = \widehat{BEC}\) (hai góc đối đỉnh)

Do đó ΔAED ∽ ΔBEC (c.g.c)

Bài 9.16

Cho hình thang ABCD (AB//CD và các điểm M, N lần lượt trên cạnh AD và BC sao cho \(2AM=MD\), \(2BN=NC\). Biết \(AB=5cm, CD=6cm\). Hãy tính độ dài đoạn thẳng MN.

Lời giải:

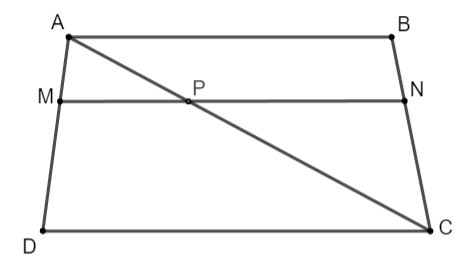
Kẻ đường thẳng qua M, song song với DC và cắt AC tại P.

Xét tam giác ADC có MP // DC (1) nên \(\frac{AM}{MD}=\frac{AP}{PC}=\frac{1}{2}\) (định lí Thales)

Xét tam giác ABC có \(\frac{AP}{PC}=\frac{AP}{PC}=\frac{1}{2}\), suy ra PN // AB (định lí Thales đảo) (2)

Mặt khác AB // CD (gt) (3)

Từ (1), (2) và (3) suy ra MP và PN trùng nhau, hay M, P, N thẳng hàng.

Ta có ΔAMP ∽ ΔADC (vì MP // DC) nên \(\frac{MP}{DC}=\frac{AM}{AD}=\frac{1}{3}\)

Suy ra \(MP=\frac{DC}{3}=\frac{6}{3}=2\) cm

Tương tự, ΔCPN ∽ ΔCAB (vì PN // AB) nên \(\frac{PN}{AB}=\frac{CN}{CB}=\frac{2}{3}\)

Suy ra \(PN=\frac{2AB}{3}=\frac{2.5}{3}=\frac{10}{3}\) cm

Vậy \(MN=MP+PN=2+\frac{10}{3}=\frac{16}{3}\) (cm).