Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác Giải Toán 8 Cánh diều tập 2 trang 58, 59, 60, 61

Giải Toán 8 Bài 2: Ứng dụng của định lí Thalès trong tam giác là tài liệu vô cùng hữu ích giúp các em học sinh lớp 8 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 8 Cánh diều tập 2 trang 58, 59, 60, 61.

Giải bài tập Toán 8 Cánh diều tập 2 trang 58 → 61 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 2 Chương VIII: Tam giác đồng dạng, hình đồng dạng. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 8 Cánh diều Tập 2 trang 60, 61

Bài 1

Để đo khoảng cách giữa hai vị trí A và B trong đo B không tới được, người ta tiến hành chọn các vị trí C, D, E như ở Hình 24 và đo được AC = 50 m, CD = 20 m, DE = 18 m. Hỏi khoảng cách giữa hai vị trí A và B là bao nhiêu?

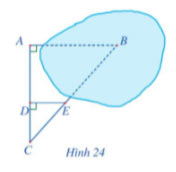
Lời giải:

Ta có: DE // AB (cùng vuông góc với AC)

Suy ra: \(\frac{CD}{AC}=\frac{DE}{AB}\) hay \(\frac{20}{50}=\frac{18}{AB}\)

Do đó: AB = 45. Vậy khoảng cách giữa hai vị trí A và B là 45 m.

Bài 2

Có thể gián tiếp đo chiều cao của một bức tường khá cao bằng dụng cụ đơn giản được không?

Hình 25 thể hiện cách đo chiều cao AB của một bức tường bằng các dụng cụ đơn giản gồm: hai cọc thẳng đứng (cọc 1 cố định; cọc 2 có thể di động được) và sợi dây FC. Cọc 1 có chiều cao DK = h. Các khoảng cách BC = a, DC = b đo được bằng thước dây thông dụng.

a) Em hãy cho biết người ta tiến hành đo đạc như thế nào?

b) Tính chiều cao AB theo h, a, b.

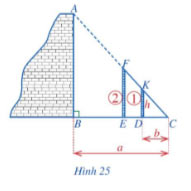
Lời giải:

a) Vì cọc 2 di động được nên di chuyển cọc 2 sao cho cọc 2 trùng với AB, cụ thể F trùng với A, E trùng với B.

Lúc này cọc 1 song song với AB. Do đó, ta có tỉ lệ giữa cọc 1 và AB bằng với tỉ lệ giữa khoảng cách DC và BC. Từ đó ta tính được chiều cao AB của bức tường.

b) Ta có: \(\frac{DK}{AB}=\frac{DC}{BC}\) hay \(\frac{h}{AB}=\frac{b}{a}\)

Suy ra: AB = \(\frac{ah}{b}\).

Bài 3

Trong Hình 26, các thanh AA', BB', CC', DD' của giàn gỗ song song với nhau. Không sử dụng thước đo, hãy giải thích vì sao độ dài các đoạn AB, BC, CD lần lượt tỉ lệ với độ dài các đoạn A'B', B'C', C'D'.

Lời giải:

Bài tập 2 trang 57 cho ta kết quả: Đường thẳng song song với hai đáy của hình thang thì định ra trên hai cạnh bên các đoạn thẳng tỉ lệ.

Do đó áp dụng vào bài tập này ta có:

Hình thang ACC'A' (AA' // CC') có BB' song song với hai đáy nên suy ra: \(\frac{AB}{BC}=\frac{A'B'}{B'C'}\) hay \(\frac{AB}{A'B'}=\frac{BC}{B'C'}\) (1)

Hình thang BB'D'D (BB' // CC') có CC' song song với hai đáy nên suy ra: \(\frac{BC}{CD}=\frac{B'C'}{C'D'}\) hay \(\frac{BC}{B'C'}=\frac{CD}{C'D'}\) (2)

Từ (1)(2) suy ra: \(\frac{AB}{A'B'}=\frac{BC}{B'C'}=\frac{CD}{C'D'}\).

Bài 4

Anh Thiện và chị Lương đứng ở hai phía bờ sông và muốn ước lượng khoảng cách giữa hai vị trí A, B ở hai bên bờ sông (Hình 27).

- Anh Thiện chọn vị trí C ở trên bờ sông sao cho A, B, C thẳng hàng và đo được BC = 4 m.

- Tiếp theo, anh Thiện xác định vị trí D, chị Lương xác định vị trí E sao cho D, B, E thẳng hàng, đồng thời \(\widehat{BAE}=\widehat{BCD}=90^{\circ}\).

- Anh Thiện đo được CD = 2 m, chị Lương đo được AE = 12 m.

Hãy tính khoảng cách giữa hai vị trí A và B.

Lời giải:

Vì \(\widehat{BAE}=\widehat{BCD}=90^{\circ}\) nên AC vuông góc với AE, AC vuông góc với CD.

Suy ra: CD // AE.

Ta có tỉ lệ: \(\frac{BC}{BA}=\frac{CD}{AE}\) hay \(\frac{4}{BA}=\frac{2}{12}\)

Do đó: AB = 24. Vậy khoảng cách giữa hai vị trí A và B bằng 24 m.