Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn Giải Toán 9 Kết nối tri thức tập 1 trang 5, 6, 7, 8, 9, 10

Giải bài tập Toán 9 Bài 1: Khái niệm phương trình và hệ hai phương trình bậc nhất hai ẩn với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9 Tập 1 Kết nối tri thức trang 5, 6, 7, 8, 9, 10. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 9 Bài 1 chi tiết phần câu hỏi, luyện tập, bài tập, đồng thời còn giúp các em hệ thống lại toàn bộ kiến thức trọng tâm của Bài 1 Chương I: Phương trình và hệ hai phương trình bậc nhất hai ẩn. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Vậy mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Phần Luyện tập

Luyện tập 1 trang 6 Toán 9 tập 1

Hãy viết một phương trình bậc nhất hai ẩn và chỉ ra một nghiệm của nó. 

Hướng dẫn giải:

Ta có \(2x - y = 5\) là một phương trình bậc nhất hai ẩn.

Cặp số \(\left( {3;1} \right)\) là một nghiệm của phương trình \(2x - y = 5\) vì \(2.3 - 1 = 5.\) (luôn đúng).

Luyện tập 2 trang 8 Toán 9 tập 1

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – 3y = 5;

b) 0x + y = 3;

c) x + 0y = −2.

Hướng dẫn giải:

a) 2x – 3y = 5 (1)

Ta viết (1) dưới dạng \(y=\frac{2}{3}x-\frac{5}{3}\). Mỗi cặp số \(\left(x;\ \frac{2}{3}x-\frac{5}{3}\right)\) với x ∈ R tùy ý, là một nghiệm của (1).

Khi đó ta nói phương trình (1) có nghiệm (tổng quát) là:

\(\left(x;\ \frac{2}{3}x-\frac{5}{3}\right)\) với x ∈ R tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng \(y=\frac{2}{3}x-\frac{5}{3}\). Ta cũng gọi đường thẳng này là đường thẳng d: 2x - 3y = 5.

Ta xác định hai điểm tùy ý của d là A(\(\frac{5}{2}\); 0) và B(0; \(-\frac{5}{3}\)).

Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 2x - 3y = 5 như sau:

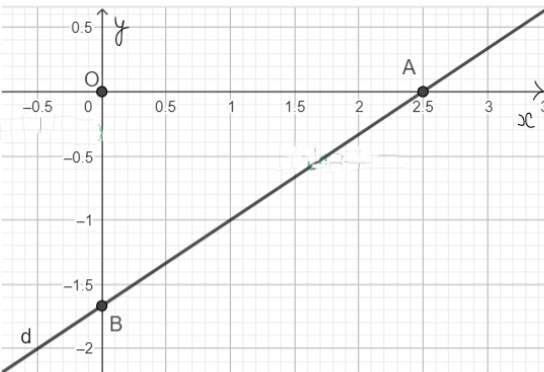
b) 0x + y = 3 (2)

Ta viết gọn (2) thành y = 3. Phương trình (2) có nghiệm là (x; 3) với x ∈ R tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm C(0; 3). Ta gọi đó là đường thẳng y = 3.

Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn 0x + y = 3 như sau:

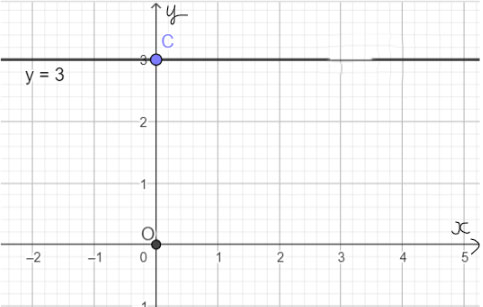
c) x + 0y = −2 (3)

Ta viết gọn (3) thành x = - 2. Phương trình (3) có nghiệm là (- 2; y) với y ∈ R tùy ý.

Mỗi nghiệm này là tọa độ của một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm D(- 2; 0). Ta gọi đó là đường thẳng x = - 2.

Ta biểu diễn hình học tất cả các nghiệm của phương trình bậc nhất hai ẩn x + 0y = −2 như sau:

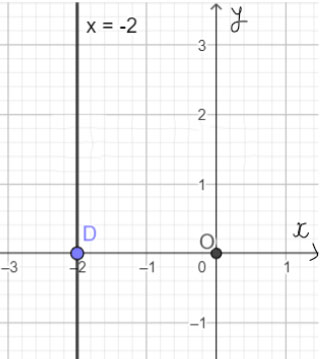
Luyện tập 3 trang 9 Toán 9 tập 1

Trong hai cặp số \(\left( {0; - 2} \right)\) và \(\left( {2; - 1} \right),\) cặp số nào là nghiệm của hệ phương trình

\(\left\{ \begin{array}{l}x - 2y = 4\\4x + 3y = 5\end{array} \right.?\)

Hướng dẫn giải:

Thay \(\left( {0; - 2} \right)\) vào hệ đã cho ta có:

\(\left\{ \begin{array}{l}0 - 2.\left( { - 2} \right) = 4\\4.0 + 3\left( { - 2} \right) = 5\end{array} \right.\) (vô lí)

Nên \(\left( {0; - 2} \right)\) không là nghiệm của hệ phương trình đã cho.

Thay \(\left( {2; - 1} \right)\) vào hệ đã cho ta có:

\(\left\{ \begin{array}{l}2 - 2.\left( { - 1} \right) = 4\\4.2 + 3\left( { - 1} \right) = 5\end{array} \right.\) (luôn đúng)

Nên \(\left( {2; - 1} \right)\) là nghiệm của hệ phương trình đã cho.

Phần Bài tập

Bài 1.1 trang 10 Toán 9 tập 1

Phương trình nào sau đây là phương trình bậc nhất hai ẩn? Vì sao?

a) 5x – 8y = 0;

b) 4x + 0y = –2;

c) 0x + 0y = 1;

d) 0x – 3y = 9.

Lời giải:

a) Phương trình 5x – 8y = 0 có dạng ax + by = c với a = 5 ≠ 0, b = –8 ≠ 0.

Do đó, phương trình 5x – 8y = 0 là phương trình bậc nhất hai ẩn.

b) Phương trình 4x + 0y = –2 có dạng ax + by = c với a = 4 ≠ 0.

Do đó, phương trình 4x + 0y = –2 là phương trình bậc nhất hai ẩn.

c) Phương trình 0x + 0y = 1 có dạng ax + by = c với a = 0, b = 0.

Do đó, phương trình 0x + 0y = 1 không phải là phương trình bậc nhất hai ẩn.

d) Phương trình 0x – 3y = 9 có dạng ax + by = c với b = –3 ≠ 0.

Do đó, phương trình 0x – 3y = 9 là phương trình bậc nhất hai ẩn.

Bài 1.2 trang 10 Toán 9 tập 1

a) Tìm giá trị thích hợp thay cho dấu "?" trong bảng sau rồi cho biết 6 nghiệm của phương trình 2x – y = 1:

b) Viết nghiệm tổng quát của phương trình đã cho.

Lời giải:

a)

• Với x = –1, ta có y = 2 . (–1) – 1 = – 2 – 1 = –3;
• Với x = –0,5, ta có y = 2 . (–0,5) – 1 = – 1 – 1 = –2;
• Với x = 0, ta có y = 2 . 0 – 1 = 0 – 1 = –1;
• Với x = 0,5, ta có y = 2 . 0,5 – 1 = 1 – 1 = 0;
• Với x = 1, ta có y = 2 . 1 – 1 = 2 – 1 = 1;
• Với x = 2, ta có y = 2 . 2 – 1 = 4 – 1 = 3.

Vậy ta có bảng sau:

Vậy 6 nghiệm của phương trình đã cho là (–1; –3), (–0,5; –2), (0; –1), (0,5; 1), (1; 1), (2; 3).

b) Ta có y = 2x – 1. Với mỗi giá trị x tùy ý cho trước, ta luôn tìm được một giá trị y tương ứng.

Do đó, phương trình đã cho có vô số nghiệm.

Bài 1.3 trang 10 Toán 9 tập 1

Viết nghiệm và biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn sau:

a) 2x – y = 3;

b) 0x + 2y = –4;

c) 3x + 0y = 5.

Lời giải:

a) Xét phương trình 2x – y = 3. (1)

Ta viết (1) dưới dạng y = 2x – 3. Mỗi cặp số (x; 2x – 3) với x ∈ ℝ tùy ý, là một nghiệm của (1).

Khi đó, ta nói phương trình (1) có nghiệm (tổng quát) là: (x; 2x – 3) với x ∈ ℝ tùy ý.

Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng y = 2x – 3.

Ta xác định được hai điểm tùy ý của đường thẳng y = 2x – 3, chẳng hạn A(0; – 3), B(1; –1).

Ta biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn như sau:

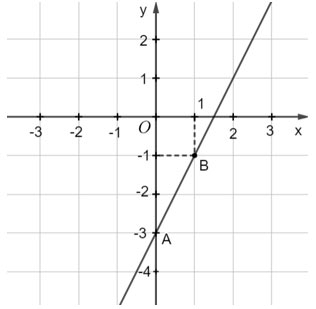
b) Xét phương trình 0x + 2y = –4 . (2)

Ta viết gọn (2) thành y = –2. Phương trình (2) có nghiệm (x; –2) với x ∈ ℝ tùy ý.

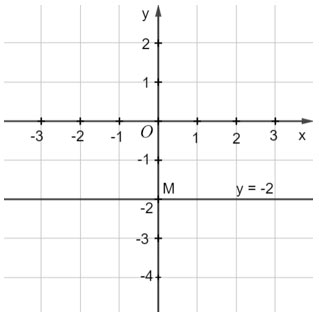
Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng song song với trục hoành và cắt trục tung tại điểm M(0; –2). Ta gọi đó là đường thẳng y = –2.

Ta biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn như sau:

c) Xét phương trình 3x + 0y = 5. (3)

Ta viết gọn (3) thành \(x=\frac{5}{3}\). Phương trình (3) có nghiệm \(\left( {\frac{5}{3};y} \right)\) với y ∈ ℝ tùy ý.

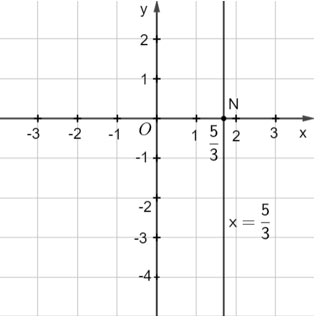
Mỗi nghiệm này là tọa độ một điểm thuộc đường thẳng song song với trục tung và cắt trục hoành tại điểm \((\frac53;0)\). Ta gọi đó là đường thẳng \(x=\frac{5}{3}\).

Ta biểu diễn hình học tất cả các nghiệm của mỗi phương trình bậc nhất hai ẩn như sau:

Bài 1.4 trang 10 Toán 9 tập 1

Cho hệ phương trình

\(\left\{ \begin{array}{l}2x = - 6\\5x + 4y = 1\end{array} \right.\)

a) Hệ phương trình trên có là một hệ hai phương trình bậc nhất hai ẩn không? Vì sao?

b) Cặp số (–3; 4) có là một nghiệm của hệ phương trình đã cho hay không? Vì sao?

Lời giải:

a) Hệ phương trình đã cho là hệ hai phương trình bậc nhất hai ẩn vì cả hai phương trình của hệ đã cho đều là phương trình bậc nhất hai ẩn.

b) Thay x = –3; y = 4 vào hệ phương trình đã cho, ta có:

• 2x = 2 . (−3) = −6 nên (–3; 4) là nghiệm của phương trình thứ nhất;

• 5x + 4y = 5 . (−3) + 4 . 4 = −15 + 16 = 1 nên (–3; 4) là nghiệm của phương trình thứ hai.

Do đó (–3; 4) là nghiệm chung của hai phương trình, nghĩa là (–3; 4) là một nghiệm của hệ phương trình đã cho.

Bài 1.5 trang 10 Toán 9 tập 1

Cho các cặp số (–2; 1), (0; 2), (1; 0), (1,5; 3), (4; –3) và hai phương trình

5x + 4y = 8, (1)

3x + 5y = –3. (2)

Trong các cặp số đã cho:

a) Những cặp số nào là nghiệm của phương trình (1)?

b) Cặp số nào là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2)?

c) Vẽ hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 trên cùng một mặt phẳng tọa độ để minh họa kết luận ở câu b.

Lời giải:

a)

• Thay x = –2; y = 1 vào phương trình (1), ta có:

5x + 4y = 5 . (–2) + 4 . 1 = −10 + 4 = −6 ≠ 8 nên (–2; 1) không phải là nghiệm của phương trình (1).

• Thay x = 0; y = 2 vào phương trình (1), ta có:

5x + 4y = 5 . 0 + 4 . 2 = 0 + 8 = 8 nên (0; 2) là nghiệm của phương trình (1).

• Thay x = 1; y = 0 vào phương trình (1), ta có:

5x + 4y = 5 . 1 + 4 . 0 = 5 + 0 = 5 ≠ 8 nên (1; 0) không phải là nghiệm của phương trình (1).

• Thay x = 1,5; y = 3 vào phương trình (1), ta có:

5x + 4y = 5 . 1,5 + 4 . 3 = 7,5 + 12 = 19,5 ≠ 8 nên (1,5; 3) không phải là nghiệm của phương trình (1).

• Thay x = 4; y = –3 vào phương trình (1), ta có:

5x + 4y = 5 . 4 + 4 . (–3) = 20 – 12 = 8 nên (4; –3) là nghiệm của phương trình (1).

Vậy cặp số là nghiệm của phương trình (1) là (0; 2) và (4; –3).

b) Để cặp số là nghiệm của hệ hai phương trình gồm phương trình (1) và phương trình (2) thì cặp số đó phải là nghiệm của phương trình (1). Khi đó, ta có:

• Thay x = 0; y = 2 vào phương trình (2), ta có:

3x + 5y = 3 . 0 + 5 . 2 = 0 + 10 = 10 ≠ –3 nên (0; 2) không phải là nghiệm của phương trình (2).

• Thay x = 4; y = –3 vào phương trình (2), ta có:

3x + 5y = 3 . 4 + 5 . (–3) = 12 – 15 = –3 nên (4; –3) là nghiệm của phương trình (2).

Ta thấy nghiệm chung của phương trình (1) và phương trình (2) là cặp số (4; –3).

Do đó, cặp số (4; –3) là nghiệm của hệ gồm phương trình (1) và phương trình (2).

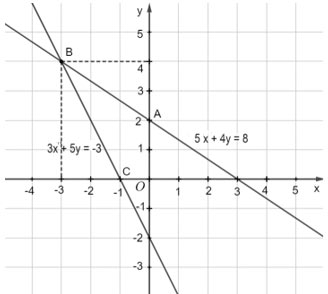
c) Đường thẳng 5x + 4y = 8 đi qua điểm A(0; 2) và B(4; –3).

Đường thẳng 3x + 5y = –3 đi qua điểm B(4; –3) và C(–1; 0).

Hai đường thẳng 5x + 4y = 8 và 3x + 5y = –3 cắt nhau tại B(4; –3), tức là (4; –3) là nghiệm của hệ (1) và (2).