Toán 9 Bài tập cuối chương VIII Giải Toán 9 Kết nối tri thức tập 2 trang 66

Giải bài tập Toán 9 Bài tập cuối chương VIII với lời giải chi tiết, rõ ràng theo khung chương trình sách giáo khoa Toán 9 Tập 2 Kết nối tri thức trang 66. Qua đó, giúp các em ôn tập và củng cố các dạng bài tập, rèn luyện kỹ năng giải môn Toán.

Giải Toán 9 chi tiết phần câu hỏi trắc nghiệm, tự luận của Bài tập cuối chương VIII: Xác suất của biến cố trong một số mô hình xác suất đơn giản. Bên cạnh đó, cũng giúp thầy cô soạn giáo án cho học sinh của mình. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 9 Kết nối tri thức Tập 2 trang 66 - Trắc nghiệm

Bài 8.12 trang 66 Toán 9 Tập 2

Gieo đồng thời hai con xúc xắc cân đối, đồng chất. Xác suất để “Tổng số chấm xuất hiện trên hai con xúc xắc lớn hơn hoặc bằng 10” là

A. \(\frac{7}{36}\)

B. \(\frac{2}{9}\)

C. \(\frac{16}{16}\)

D. \(\frac{5}{36}\)

Đáp án: C

Bài 8.13 trang 66 Toán 9 Tập 2

Có hai túi I và II. Túi I chứa 4 tấm thẻ, đánh số 1; 2; 3; 4. Túi II chứa 5 tấm thẻ, đánh số 1; 2; 3; 4; 5. Rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II. Xác suất để hai tấm thẻ rút ra đều ghi số chẵn là

A. \(\frac{1}{5}\).

B. \(\frac{3}{{20}}\).

C. \(\frac{1}{4}\).

D. \(\frac{4}{{21}}\).

Đáp án: A

Bài 8.14 trang 66 Toán 9 Tập 2

Một túi đựng 4 viên bi có cùng khối lượng và kích thước, được đánh số 1; 2; 3; 4. Lấy ngẫu nhiên hai viên bi từ trong túi. Xác suất để tích hai số ghi trên hai viên bi lớn hơn 3 là

A. \(\frac{5}{7}\).

B. \(\frac{2}{3}\).

C. \(\frac{3}{4}\).

D. \(\frac{5}{6}\).

Đáp án: B

Giải Toán 9 Kết nối tri thức Tập 2 trang 66 - Tự luận

Bài 8.15 trang 66 Toán 9 Tập 2

Có hai túi I và II. Túi I chứa 3 tấm thẻ, đánh số 2; 3; 4. Túi II chứa 2 tấm thẻ, đánh số 5; 6. Từ mỗi túi I và II, rút ngẫu nhiên một tấm thẻ. Tính xác suất của các biến cố sau:

A: “Hai số ghi trên thẻ chênh lệch nhau 2 đơn vị”;

B: “Hai số ghi trên thẻ chênh lệch nhau lớn hơn 2 đơn vị”;

C: “Tích hai số ghi trên hai tấm thẻ là một số chẵn”;

D: “Tổng hai số ghi trên hai tấm thẻ là một số nguyên tố”.

Hướng dẫn giải:

Kết quả phép thử được viết dưới dạng (a, b) trong đó a, b lần lượt là các số viết trên các thẻ trong hai túi I và II.

Do đó, không gian mẫu là: \(\operatorname\Omega\;={\{{(2,5)},{(2,6)},{(3,5)},{(3,6)},{(4,5)},{(4,6)}\}}\) nên số phần tử của không gian mẫu \(\Omega\) là 6.

Vì rút ngẫu nhiên một tấm thẻ từ mỗi túi I và II nên các kết quả có thể xảy ra ở trên là đồng khả năng.

Có 2 kết quả thuận lợi của biến cố A là: (4, 6), (3, 5). Do đó, \(P\left( A \right) = \frac{2}{6} = \frac{1}{3}\).

Có 3 kết quả thuận lợi của biến cố B là: (2, 5), (2, 6), (3, 6). Do đó, \(P\left( B \right) = \frac{3}{6} = \frac{1}{2}\).

Có 5 kết quả thuận lợi của biến cố C là: (2, 5), (2, 6), (3, 6), (4, 5), (4, 6). Do đó, \(P\left( C \right) = \frac{5}{6}\).

Có 1 kết quả thuận lợi của biến cố D là: (2, 5). Do đó, \(P\left( D \right) = \frac{1}{6}\).

Bài 8.16 trang 66 Toán 9 Tập 2

Gieo đồng thời hai con xúc xắc cân đối, đồng chất I và II. Tính xác suất của các biến cố sau:

E: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 11”;

F: “Tổng số chấm xuất hiện trên hai con xúc xắc bằng 8 hoặc 9”;

G: “Tổng số chấm xuất hiện trên hai con xúc xắc nhỏ hơn 6”.

Hướng dẫn giải:

Ta có bảng miêu tả không gian mẫu là:

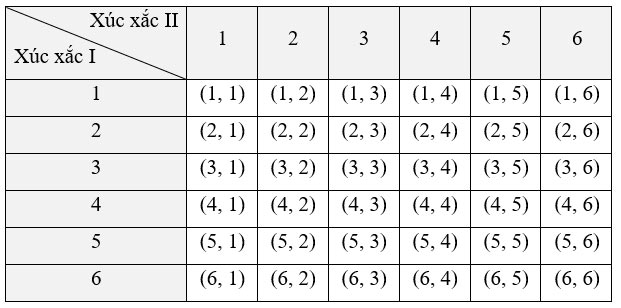
Do đó, số phần tử của không gian mẫu \(\Omega\) là 36.

Vì gieo đồng thời hai con xúc xắc cân đối, đồng chất nên các kết quả có thể xảy ra là đồng khả năng.

Có 2 kết quả thuận lợi của biến cố E là: (5, 6), (6, 5). Do đó, \(P\left( E \right) = \frac{2}{{36}} = \frac{1}{{18}}\).

Có 9 kết quả thuận lợi của biến cố F là: (2, 6), (3, 5), (3, 6), (4, 4), (4, 5), (5, 3), (5, 4), (6, 2), (6, 3). Do đó, \(P\left( F \right) = \frac{9}{{36}} = \frac{1}{4}\).

Có 10 kết quả thuận lợi của biến cố G là: (1, 1), (1, 2), (1, 3), (1, 4), (2, 1), (2, 2), (2, 3), (3, 1), (3, 2), (4, 1). Do đó, \(P\left( F \right) = \frac{{10}}{{36}} = \frac{5}{{18}}\).

Bài 8.17 trang 66 Toán 9 Tập 2

Hai bạn Minh và Huy chơi một trò chơi như sau: Minh chọn ngẫu nhiên một số trong tập hợp {5; 6; 7; 8; 9; 10}; Huy chọn ngẫu nhiên một số trong tập hợp {4; 5; 7; 8; 9; 11}. Bạn nào chọn được số lớn hơn sẽ là người thắng cuộc. Nếu hai số chọn được bằng nhau thì kết quả là hoà. Tính xác suất của các biến cố sau:

a) A: “Bạn Minh thắng”;

b) B: “Bạn Huy thắng”.