Toán 7 Bài 9: Đường trung trực của một đoạn thẳng Giải Toán lớp 7 trang 100, 101, 102 - Tập 2 sách Cánh diều

Giải Toán 7 Bài 9: Đường trung trực của một đoạn thẳng Cánh diều là tài liệu vô cùng hữu ích giúp các em học sinh lớp 7 có thêm nhiều gợi ý tham khảo để giải các bài tập từ 1→4 trang 100, 101, 102 tập 2.

Giải bài tập Toán 7 Cánh diều tập 2 trang 100, 101, 102 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài, đồng thời là tư liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy sau đây là nội dung chi tiết Giải Toán 7 bài 9 trang 100, 101, 102 Cánh diều, mời các bạn cùng theo dõi.

Giải Toán 7 trang 100, 101, 102 Cánh diều - Tập 2

Bài 1 

Trong Hình 94, đường thẳng CD là đường trung trực của đoạn thẳng AB. Chứng minh \(\widehat {CAD} = \widehat {CBD}.\)

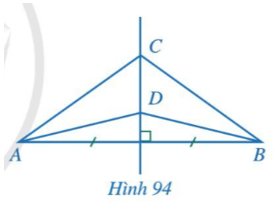
Gợi ý đáp án

Ta có: đường thẳng CD là đường trung trực của đoạn thẳng AB. Nên CD đi qua trung điểm của AB và vuông góc với AB.

Hay \(\widehat {CAB} = \widehat {CBA}\); \(\widehat {DAB} = \widehat {DBA}.\)

Vậy \(\widehat {CAB} - \widehat {DAB} = \widehat {CBA} - \widehat {DBA}\) suy ra:\(\widehat {CAD} = \widehat {CBD}.\)

Bài 2

Trong Hình 95, đường thẳng a là đường trung trực của cả hai đoạn thẳng AB và CD.

Chứng minh:

a) AB // CD;

b) ∆MNC = ∆MND;

c) \(\hat{AMD} = \hat{BMC}\)

d) AD = BC, \(\hat{A} = \hat{B}\)

e) \(\hat{ADC} = \hat{BCD}\)

Gợi ý đáp án

a) Do a là đường trung trực của cả hai đoạn thẳng AB và CD nên a ⊥ AB và a ⊥ CD.

Do đó AB // CD.

b) Xét ∆MNC vuông tại N và ∆MND vuông tại N có:

MN chung.

NC = ND (theo giả thiết).

Do đó ∆MNC = ∆MND (2 cạnh góc vuông).

c) Do ∆MNC = ∆MND (2 cạnh góc vuông) nên \(\hat{MCN} = \hat{MDN}\) (2 góc tương ứng)

Do AM // DN nên \(\hat{AMD} = \hat{MDN}\) (2 góc so le trong).

Do BM // CN nên \(\hat{BMC} = \hat{MCN}\) (2 góc so le trong).

Do đó \(\hat{AMD} = \hat{BMC}\)

d) Do ∆MNC = ∆MND (2 cạnh góc vuông) nên MC = MD (2 cạnh tương ứng).

Xét ∆AMD và ∆BMC có:

AM = BM (theo giả thiết).

\(\hat{AMD} = \hat{BMC}\) (chứng minh trên).

MD = MC (chứng minh trên).

Do đó ∆AMD = ∆BMC (c - g - c).

Suy ra AD = BC (2 cạnh tương ứng) và \(\hat{MAD} = \hat{MBC}\) (2 góc tương ứng).

Vậy AD = BC và \(\hat{A} = \hat{B}\)

e) Do ∆AMD = ∆BMC (c - g - c) nên \(\hat{AMD} = \hat{BMC}\) (2 góc tương ứng).

Mà \(\hat{MDN} = \hat{MCN}\) nên \(\hat{ADM} + \hat{MDN} = \hat{BCM} + \hat{MCN}\) hay \(\hat{ADC} = \hat{BCD}\)

Bài 3

Cho ba điểm A, B, C thẳng hàng, điểm B nằm giữa hai điểm A và C. Gọi a và b lần lượt là đường trung trực của các đoạn thẳng AB và BC. Chứng minh rằng a // b.

Gợi ý đáp án

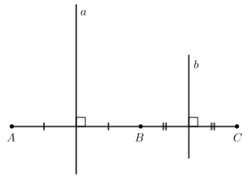
a là đường trung trực của đoạn thẳng AB nên a vuông góc với AB tại trung điểm của AB.

b là đường trung trực của đoạn thẳng BC nên b vuông góc với BC tại trung điểm của BC.

Do A, B, C thẳng hàng và B nằm giữa A và C nên trung điểm của đoạn thẳng AB và trung điểm của đoạn thẳng BC không trùng nhau.

Do đó a // b.

Bài 4 

Cho đường thẳng d là đường trung trực của đoạn thẳng AB. Điểm M không thuộc đường thẳng d và đoạn thẳng AB sao cho đường thẳng d cắt đoạn thẳng MB tại điểm I. Chứng minh:

a) MB = AI + IM;

b) MA < MB.

Gợi ý đáp án

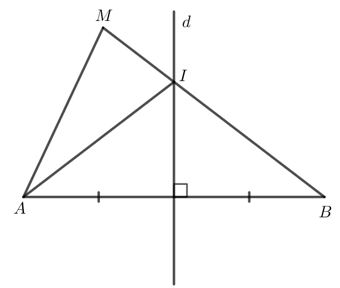
a) Đường thẳng d cắt MB tại I nên I thuộc đường trung trực của đoạn thẳng AB.

Do đó AI = BI.

Khi đó MB = BI + IM = AI + IM.

b) Xét trong tam giác AIM có AI + IM > MA.

Mà AI + IM = MB nên MB > MA.