Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn Giải Toán 9 Cánh diều tập 1 trang 74, 75, 76, 77, 78, 79, 80, 81
Giải Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn là tài liệu vô cùng hữu ích giúp các em học sinh lớp 9 có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 9 Cánh diều tập 1 trang 74, 75, 76, 77, 78, 79, 80, 81.
Giải bài tập Toán 9 Cánh diều tập 1 Bài 1 - Chương IV: Hệ thức lượng trong tam giác vuông được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh học tập. Vậy mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 9 Bài 1: Tỉ số lượng giác của góc nhọn Cánh diều
Giải Toán 9 Cánh diều Tập 1 trang 81
Bài 1
Cho tam giác ABC vuông tại A có AC = 4 cm, BC = 6 cm. Tính các tỉ số lượng giác của góc B.
Bài 2
Cho tam giác ABC vuông tại A có AB = 2 cm, AC = 3 cm. Tính các tỉ số lượng giác của góc C.
Bài 3
Cho tam giác MNP có MN = 5 cm, MP = 12 cm, NP = 13 cm. Chứng minh tam giác MNP vuông tại M. Từ đó, tính các tỉ số lượng giác của góc N.
Hướng dẫn giải:
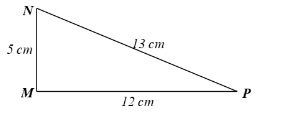
Xét ∆MNP, ta có: NP2 = 132 = 169 và MN2 + MP2 = 52 + 122 = 169.
Suy ra NP2 = MN2 + MP2.
Do đó ∆MNP vuông tại M (định lí Pythagore đảo).
Khi đó:
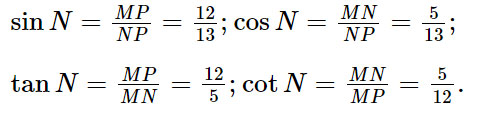
Bài 4
Mỗi tỉ số lượng giác sau đây bằng tỉ số lượng giác nào của góc 63°? Vì sao?
a) sin27°;
b) cos27°;
c) tan27°;
d) cot27°.
Hướng dẫn giải:
Vì 27° và 63° là hai góc phụ nhau nên ta có:
a) sin27° = cos63°;
b) cos27° = sin63°;
c) tan27° = cot63°;
d) cot27° = tan63°.
Bài 5
Sử dụng máy tính cầm tay để tính các tỉ số lượng giác của mỗi góc sau (làm tròn kết quả đến hàng phần trăm):
a) 41°;
b) 28°35’;
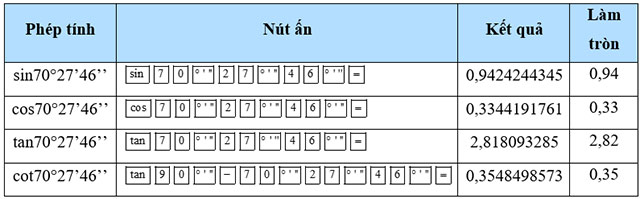
c) 70°27’46’’.
Hướng dẫn giải:
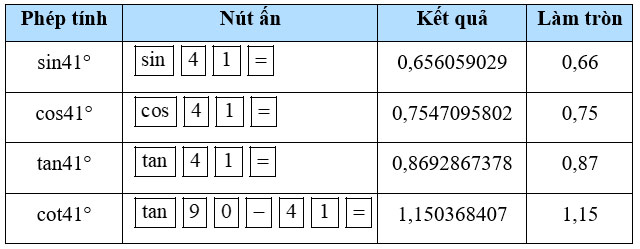
b)
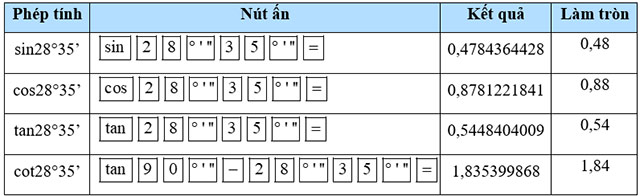
c)
Bài 6
Sử dụng tỉ số lượng giác của hai góc phụ nhau, tính giác trị biểu thức:
A = sin25° + cos25° – sin65° – cos65°.
Hướng dẫn giải:
Vì25° và 65° là hai góc phụ nhau nên ta có sin25° = cos65° và sin65° = cos25°.
Do đó:
A = sin25° + cos25° – sin65° – cos65°
= cos65° + cos25° – cos25° – cos65°
= 0.
Bài 7
Cho góc nhọn α. Biết rằng, tam giác ABC vuông tại A có ![]() \(\widehat {B} =α\)
\(\widehat {B} =α\)
a) Biểu diễn các tỉ số lượng giác của góc nhọn α theo AB, BC, CA.
b) Chứng minh:
sin2α+cos2α = 1; ![]() \(\tan\ α=\frac{\sinα}{\cosα};\cos\ α=\frac{\cosα}{\sinα};\tan\ α.\cos\ α=1\)
\(\tan\ α=\frac{\sinα}{\cosα};\cos\ α=\frac{\cosα}{\sinα};\tan\ α.\cos\ α=1\)
Từ đó, tính giá trị biểu thức: S = sin235° + cos235°; T = tan61°.cot61°.
Bài 8
Hình 10 mô tả tia nắng mặt trời dọc theo AB tạo với phương nằm ngang trên mặt đất một góc α = ![]() \(\widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.
\(\widehat {ABH}\). Sử dụng máy tính cầm tay, tính số đo góc α (làm tròn kết quả đến hàng đơn vị của độ) biết AH = 2 m, BH = 5 m.
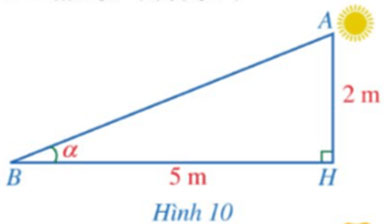
Hướng dẫn giải:
Xét ∆ABH vuông tại H, ta có tanα = tanB = ![]() \(\frac{AH}{BH}\) =
\(\frac{AH}{BH}\) = ![]() \(\frac{2}{5}\)
\(\frac{2}{5}\)
Suy ra α ≈ 22°.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Công thức tính đường cao trong tam giác
-

Bài thu hoạch thăng hạng giáo viên Mầm non hạng II (3 mẫu)
-

Đoạn văn tiếng Anh hướng dẫn để cho trường học bạn xanh hơn
-

Cảm xúc về bài hát Như có Bác trong ngày đại thắng (6 mẫu)
-

Điều lệ Trường Mầm non - Ban hành kèm theo Thông tư số 52/2020/TT-BGDĐT
-

Kể lại truyền thuyết Sơn Tinh, Thủy Tinh bằng lời văn của em (2 Dàn ý + 21 mẫu)
-

Bài thu hoạch những nội dung chính trong công tác xây dựng Đảng ở cơ sở hiện nay
-

Ma trận đề thi học kì 2 lớp 5 năm 2024 - 2025 theo Thông tư 27
-

Tả cơn mưa rào mùa hạ - 3 Dàn ý & 35 bài văn tả cơn mưa lớp 5
-

Mẫu sáng kiến kinh nghiệm chuẩn - Mẫu sáng kiến kinh nghiệm dành cho giáo viên
Mới nhất trong tuần
-

Các dạng bài tập Toán 9 Cánh diều (Cả năm)
100+ -

Toán 9 Bài 2: Một số phép tính về căn bậc hai của số thực
100.000+ -

Toán 9 Bài 1: Phương trình quy về phương trình bậc nhất một ẩn
1.000+ -

Toán 9 Bài tập cuối chương V
100+ -

Toán 9 Bài 5: Độ dài cung tròn, diện tích hình quạt tròn, diện tích hình vành khuyên
1.000+ -

Toán 9 Bài 4: Góc ở tâm. Góc nội tiếp
1.000+ -

Toán 9 Bài 3: Tiếp tuyến của đường tròn
100+ -

Toán 9 Bài 2: Vị trí tương đối của đường thẳng và đường tròn
100+ -

Toán 9 Bài 1: Đường tròn. Vị trí tương đối của hai đường tròn
100+ -

Toán 9 Bài tập cuối chương IV
100+






 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức