Toán 7 Bài tập cuối chương 4 - Chân trời sáng tạo Giải Toán lớp 7 trang 86, 87 - Tập 1

Giải Toán lớp 7 Bài tập cuối chương 4 bao gồm đáp án chi tiết, cùng hướng dẫn giải các bài tập trong SGK Toán 7 Tập 1 Chân trời sáng tạo trang 86, 87.

Lời giải Toán 7 Chân trời sáng tạo trình bày khoa học, biên soạn dễ hiểu, giúp các em nâng cao kỹ năng giải Toán 7, từ đó học tốt môn Toán lớp 7 hơn. Đồng thời, cũng giúp thầy cô nhanh chóng soạn giáo án Bài tập cuối chương IV - Góc và đường thẳng song song. Mời thầy cô và các em cùng theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 7 Chân trời sáng tạo trang 86, 87 tập 1

Bài 1

Trong những câu sau, em hãy chọn những câu đúng.

Tia Oz là tia phân giác của góc \(\widehat {xOy}\) khi:

\(\begin{array}{l}a)\widehat {xOz} = \widehat {yOz}\\b)\widehat {xOz} + \widehat {yOz} = \widehat {xOy}\\c)\widehat {xOz} = \widehat {yOz} = \frac{{\widehat {xOy}}}{2}\end{array}\)

Hướng dẫn giải:

Tia phân giác của một góc là tia xuất phát từ một đỉnh của góc, đi qua một điểm trong của góc và tạo với hai cạnh của góc đó hai góc bằng nhau.

Gợi ý đáp án:

Hình vẽ minh họa:

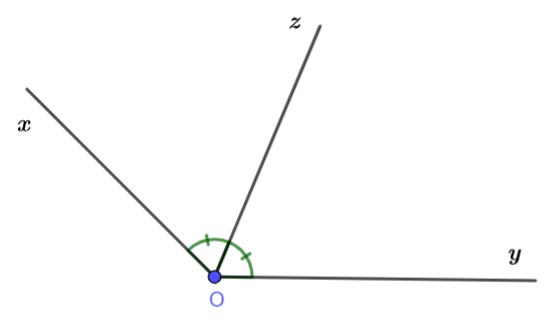
a) Do Oz là tia phân giác của góc xOy => \(\widehat {xOz} = \widehat {yOz}\)

=> Khẳng đính đúng

b) Do tia Oz là tia nằm giữa hai tia Ox và Oy và chung gốc O.

=> \(\widehat {xOz} + \widehat {zOy} = \widehat {xOy}\)

=> Khẳng định đúng

c) Ta có: Oz là tia phân giác của góc xOy

=> \(\widehat {xOz} = \widehat {yOz} = \frac{{\widehat {xOy}}}{2}\)

Khẳng định đúng

Bài 2

Quan sát Hình 1, biết d // h. Hãy kể tên một số cặp góc bằng nhau có trong Hình 1

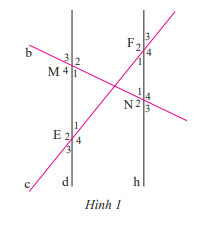
Hướng dẫn giải:

- Nếu đường thẳng c cắt hai đường thẳng, b và trong các góc tạo thành có mộ t cặp góc so le trong bằng nhau (hoặc một cặp góc đồng vị bằng nhau) thì a và b song song với nhau.

- Qua một điểm nằm ngoài một đường thẳng chỉ có một đường thẳng song song với đường thẳng đó.

- Nếu một đường thẳng cắt hai đường thẳng song song thì: Hai góc so le trong bằng nhau và hai góc đồng vị bằng nhau.

Gợi ý đáp án:

Ta có: \(\widehat {{M_1}} = \widehat {{M_3}};\widehat {{M_2}} = \widehat {{M_4}}\) (các góc đối đỉnh)

\(\widehat {{E_1}} = \widehat {{E_3}};\widehat {{E_2}} = \widehat {{E_4}}\)(các góc đối đỉnh)

\(\widehat {{N_1}} = \widehat {{N_3}};\widehat {{N_2}} = \widehat {{N_4}}\) (các góc đối đỉnh)

\(\widehat {{F_1}} = \widehat {{F_3}};\widehat {{F_2}} = \widehat {{F_4}}\) (các góc đối đỉnh)

Vì d // h nên:

+) \(\widehat {{M_1}} = \widehat {{N_1}};\widehat {{M_2}} = \widehat {{N_2}};\widehat {{E_1}} = \widehat {{F_1}};\widehat {{E_2}} = \widehat {{F_2}}\) (các góc so le trong)

+) \(\widehat {{M_1}} = \widehat {{N_3}};\widehat {{M_2}} = \widehat {{N_4}}; \widehat {{M_3}} = \widehat {{N_1}};\widehat {{M_4}} = \widehat {{N_2}}; \widehat {{E_1}} = \widehat {{F_3}};\widehat {{E_2}} = \widehat {{F_4}};\widehat {{E_3}} = \widehat {{F_1}};\widehat {{E_4}} = \widehat {{F_2}}\) (các góc đồng vị)

Bài 3

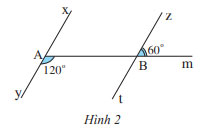
Quan sát Hình 2.

Chứng minh rằng xy // zt

Gợi ý đáp án:

Vì \(\widehat {{A_1}} + \widehat {{A_2}} = 180^\circ\)(2 góc kề bù) nên \(\widehat {{A_1}} + 120^\circ = 180^\circ \Rightarrow \widehat {{A_1}} = 180^\circ - 120^\circ = 60^\circ\)

Ta có: \(\widehat {{A_1}} = \widehat {{B_1}}( = 60^\circ )\). Mà 2 góc này ở vị trí đồng vị

Nên xy // zt

Bài 4

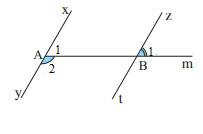
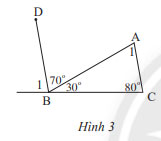
Quan sát Hình 3

a) Tính B1

b) Chứng minh rằng AC // BD

c) Tính A2

Gợi ý đáp án:

a) Vì \(\widehat {{B_1}} + 70^\circ + 30^\circ = 180^\circ\)(kề bù) nên \(\widehat {{B_1}} = 80^\circ\)

b) Vì \(\widehat {{B_1}} = \widehat {{A_1}}( = 80^\circ )\), mà 2 góc này ở vị trí so le trong nên AC // BD (Dấu hiệu nhận biết 2 đường thẳng song song)

c) Vì AC // BD nên \(\widehat {DBA} = \widehat {{A_1}}\) (2 góc so le trong), mà \(\widehat {DBA} = 70^\circ \Rightarrow \widehat {{A_1}} = 70^\circ\)

Bài 5

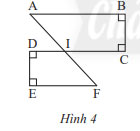
Quan sát Hình 4. Chứng minh rằng:

a) AB // CD và EF // CD

b) AB // EF

Gợi ý đáp án:

a) Vì \(AB \bot BC;CD \bot BC \Rightarrow AB//CD\) (cùng vuông góc với BC)

Vì \(EF \bot DE;CD \bot DE \Rightarrow EF//CD\) (cùng vuông góc với DE)

b) Vì \(AB // CD\) và \(EF // CD\) nên \(AB // EF\) (cùng song song với CD)

Bài 6

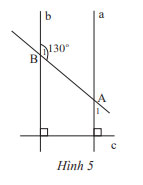
Cho Hình 5 có \(\widehat {{B_1}} = 130^\circ\). Số đo của \(\widehat {{A_1}}\) là bao nhiêu?

Gợi ý đáp án:

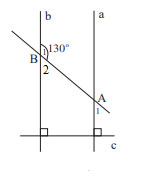
Vì a \bot c, b \bot c nên a // b (cùng vuông góc với c)

Ta có: \(\widehat {{B_1}} + \widehat {{B_2}} = 180^\circ\)(2 góc kề bù) nên \(130^\circ + \widehat {{B_2}} = 180^\circ \Rightarrow \widehat {{B_2}} = 180^\circ - 130^\circ = 50^\circ\)

Vì a // b nên \(\widehat {{A_1}} = \widehat {{B_2}}\)(2 góc đồng vị) nên \(\widehat {{A_1}} = 50^\circ\)

Bài 7

Cho Hình 6, biết hai đường thẳng a và b song song với nhau và \(\widehat {{A_1}} = 50^\circ\)

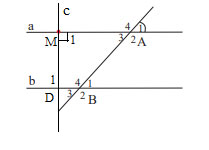
a) Hãy viết tên các cặp góc so le trong và các cặp góc đồng vị.

b) Tính số đo của \(\widehat {{A_3}},\widehat {{B_3}}\)

c) Kẻ đường thẳng c vuông góc với đường thẳng a tại M. Chứng minh rằng c \bot b.

Gợi ý đáp án:

a) Các cặp góc so le trong là: \(\widehat {{A_3}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_4}}\)

Các cặp góc đồng vị là: \(\widehat {{A_1}} = \widehat {{B_1}};\widehat {{A_2}} = \widehat {{B_2}};\widehat {{A_3}} = \widehat {{B_3}};\widehat {{A_4}} = \widehat {{B_4}}\)

b) Vì \(\widehat {{A_1}} = \widehat {{A_3}}\) (2 góc đối đỉnh), mà \(\widehat {{A_1}} = 50^\circ\) nên

Vì a // b nên \(\widehat {{A_3}} = \widehat {{B_3}}\)(2 góc đồng vị), mà \(\widehat {{A_3}} = 50^\circ\) nên \(\widehat {{B_3}} = 50^\circ\)

c) Gọi c cắt b tại D

Vì a // b nên \(\widehat {{M_1}} = \widehat {{D_1}}\) (2 góc so le trong), mà \(\widehat {{M_1}} = 90^\circ \Rightarrow \widehat {{D_1}} = 90^\circ\)

Vậy \(c \bot b\).

Chú ý: Ta có định lí: Đường thẳng vuông góc với 1 trong 2 đường thẳng song song thì cũng song song vói đường thẳng còn lại

Bài 8

Vẽ đường thẳng m song song với đường thẳng n. Vẽ đường thẳng d cắt đường thẳng m tại điểm I.

a) Hỏi nếu d // n thì điều này có trái với tiên đề Euclid không?

b) Sử dụng kết quả của câu a để chứng minh d cắt n

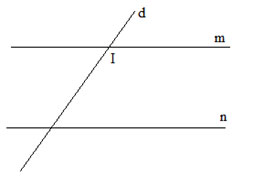
a) Nếu d // n thì qua điểm I nằm ngoài đường thẳng n, có 2 đường thẳng là m và d song song với n (Trái với tiên đề Euclid)

b) Vì d không thể song song với n (câu a) và d khác n nên d cắt n.

Chú ý:

Cách chứng minh như trên gọi là chứng minh phản chứng.