Đề thi giải toán trên Máy tính cầm tay cấp Quốc gia năm 2013 môn Toán lớp 9 THCS Bộ GD&ĐT
BỘ GIÁO DỤC VÀ ĐÀO TẠO
|
CUỘC THI GIẢI TOÁN TRÊN MÁY TÍNH CẦM TAY
|
Bài 1: (5 điểm):
Lập quy trình bấm máy và tính giá trị của mỗi biểu thức sau (Ghi đầy đủ các chữ số hiện trên máy tính):
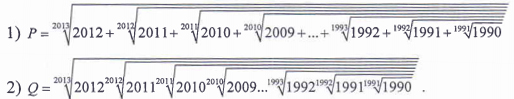
Bài 2: (5 điểm)
Một anh sinh viên được gia đình gửi vào sổ tiết kiệm ngân hàng là 80000000 đồng với lãi xuất 0,9% tháng.
1. Hỏi sau đúng 5 năm số tiền trong sổ sẽ là bao nhiêu, biết rằng trong suốt thời gian đó anh sinh viên không rút một đồng nào cả vốn lẫn lãi?
2. Nếu mỗi tháng anh sinh viên đó đều rút ra một số tiền như nhau vào ngày ngân hàng trả lãi thì hàng tháng anh ta rút ra bao nhiêu tiền (làm tròn đến 1000 đồng) để sau đúng 5 năm sẽ vừa hết số tiền cả vốn lẫn lãi.
Bài 3: (5 điểm)
Cho góc xOy = 50o. Giữa hai tia Ox, Oy lấy tia Oz sao cho góc xOz = 22o. Trên Oz lấy điểm M sao cho OM = 67cm. Một đường thẳng thay đổi luôn đi qua điểm M và cắt 2 đia Ox, Oy tương ứng tại A, B. Tính giá trị nhỏ nhất của diện tích tam giác ABO.
Bài 4: (điểm)
1. Cho biểu thức: ![]()
Tính M khi ![]() y = 26; z = 2013.
y = 26; z = 2013.
2. Tìm tất cả các số tự nhiên n trong khoảng (1000; 10000000) sao cho số ![]() là một số tự nhiên.
là một số tự nhiên.
Bài 5: (5 điểm)
Trên mặt phẳng cho trước đoạn thẳng AB. Từ điểm A vẽ đoạn thẳng AC vuông góc với AB và AC = 5,3 (cm). Từ điểm B vẽ đoạn thẳng BE vuông góc với AB (hai điểm E, C không nằm cùng phía đường thẳng AB) và BE = 7,2 (cm). Trên tia đối của tia BE lấy điểm D sao cho góc DCA bằng 65o. Gọi F là trung điểm của đoạn thẳng AE. Gọi d là đường thẳng đi qua điểm F và vuông góc với đường thẳng AE. Đường tròn tâm F bán kính FE cắt đường thẳng d tại điểm G (hai điểm B, G nằm khác phía đường thẳng AE). Biết AE = 12,4 (cm) hãy tính.
1. Độ dài đoạn thẳng BD;
2. Diện tích S của đa giác EGACD
Bài 6: (5 điểm)
Công ty Hoa Hồng thông báo quy định về trả tiền cho một trò chơi trên máy tính như sau:
A. Bạn phải trả 21000 đồng với bất kì lượng thời gian nào mà bạn chơi trò chơi.
B. Bạn phải trả 5000 đồng khi đồng ý chơi trò chơi và bạn phải trả thêm 1500 đồng cho mỗi phút chơi trò chơi.
C, Bạn phải trả 3000 đồng cho mỗi phút chơi trò chơi.
D. Bạn phải trả 15000 đồng khi đồng ý chơi trò chơi và bạn phải trả thêm 250 đồng cho mỗi phút chơi trò chơi.
Hãy cho biết bạn sẽ chơi trò chơi trên máy tính của công ty đó theo hình thức nào (Hãy ghi chữ A hay B hay C hay D vào cột hình thức chọn tương ứng với khoảng thời gian chơi của bạn) để phải trả ít tiền nhất nếu:
| Thời gian chơi | Hình thức chọn |
| 1) Bạn chơi với thời gian không quá 3 phút | |
| 2) Bạn vừa chơi với thời gian từ 3 phút 30 giây đến 5 phút | |
| 3) Bạn chơi với thời gian từ 6 phút đến 8 phút | |
| 4) Bạn chơi với thời gian từ 8 phút 30 giây đến 23 phút | |
| 5) Bạn chơi với thời gian từ 24 phút đến 60 phút |
Download tài liệu để xem thêm chi tiết
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Giáo trình quản trị mạng Windows nâng cao
-

Báo cáo ngày hội đọc sách Việt Nam năm 2025
-

Cách làm các dạng đề nghị luận văn học đạt điểm tuyệt đối trong kỳ thi THPT Quốc gia 2024
-

Văn mẫu lớp 7: Tóm tắt truyện ngắn Cuộc chia tay của những con búp bê (7 mẫu)
-

Bộ đề thi học kì 2 môn Lịch sử - Địa lý lớp 5 năm 2024 - 2025 (Sách mới)
-

Biên bản lựa chọn sách giáo khoa lớp 3
-

Bộ đề ôn thi học kì 2 môn Ngữ văn 8 năm 2023 - 2024 (Sách mới)
-

Bộ đề thi học kì 2 môn Tiếng Anh 6 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Bộ đề thi học kì 2 môn Vật lý lớp 10 năm 2024 - 2025 (Sách mới)
-

Văn mẫu lớp 10: Phân tích mâu thuẫn giữa Tấm và mẹ con Cám
Mới nhất trong tuần
-

Bộ đề kiểm tra 1 tiết Chương 1 Đại số lớp 9 (16 đề)
100.000+ -

Chứng minh phương trình luôn có nghiệm với mọi m
50.000+ -

Một số bài tập Toán nâng cao lớp 9 (Có đáp án)
10.000+ -

Bài tập hệ thức Vi-et và các ứng dụng
50.000+ -

Phân dạng và bài tập Hình học lớp 9
50.000+ 1 -

Tổng hợp các dạng bài tập Đại số lớp 9
50.000+ 1 -

Chứng minh đồ thị hàm số luôn đi qua một điểm cố định
5.000+ -

Chứng minh đẳng thức: cách chứng minh và bài tập
1.000+ -

Tìm m để hệ phương trình có nghiệm duy nhất
5.000+ -

Tìm giá trị x để A nhận giá trị nguyên
10.000+






 Đề thi giữa kì 2 lớp 9
Đề thi giữa kì 2 lớp 9
 Đề thi học kì 2 Lớp 9
Đề thi học kì 2 Lớp 9
 Đề thi giữa kì 1 lớp 9
Đề thi giữa kì 1 lớp 9
 Đề thi học kì 1 Lớp 9
Đề thi học kì 1 Lớp 9
 Toán 9
Toán 9
 Toán 9 Kết nối tri thức
Toán 9 Kết nối tri thức
 Toán 9 Cánh Diều
Toán 9 Cánh Diều
 Toán 9 Chân trời sáng tạo
Toán 9 Chân trời sáng tạo
 Văn 9 Kết nối tri thức
Văn 9 Kết nối tri thức