Thể tích khối chóp: Công thức và bài tập Ôn tập Toán 12

Khối chóp là gì? Công thức tính thể tích khối chóp như thế nào? Đây là câu hỏi được rất nhiều bạn học sinh quan tâm? Vì thế hãy cùng Eballsviet.com theo dõi bài viết dưới đây.

Trong bài viết dưới đây Eballsviet.com sẽ giới thiệu đến các bạn toàn bộ kiến thức về cách tính thể tích khối chóp kèm theo một số ví dụ minh họa có đáp án giải chi tiết. Thông qua tài liệu này giúp các bạn học sinh có thêm nhiều tư liệu ôn tập, củng cố kiến thức làm quen với các dạng bài tập Hình học. Bên cạnh đó các bạn xem thêm công thức tính chu vi hình chữ nhật, công thức tính diện tích hình vuông.

I. Hình chóp là gì? 

Hình chóp là hình có mặt đáy là một đa giác và các mặt bên là những tam giác có chung một đỉnh. Đỉnh này được gọi là đỉnh của hình chóp. Đường cao của hình chóp là đường thẳng đi qua đỉnh và vuông góc với mặt phẳng đáy.

Tên gọi của hình chóp dựa vào đa giác đáy: hình chóp tam giác có đáy là tam giác, hình chóp tứ giác có đáy là tứ giác.

II. Công thức thể tích khối chóp

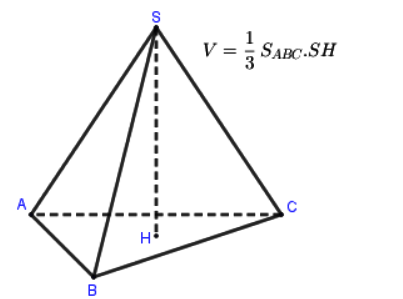
- Công thức thể tích khối chóp \(V=\frac{1}{3}.S.h\)

Trong đó: S là diện tích đáy, h là chiều cao khối chóp.

- Một phép vị tự tỉ số k biến khối đa diện có thể tích V thành khối đa diện thể tích V’ thì:\(\frac{V}{V'}={{\left| k \right|}^{3}}\)

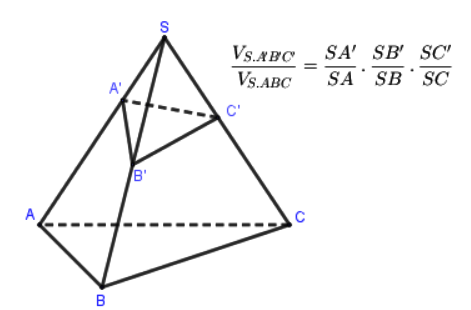
- Tỉ số thể tích hai khối chóp tam giác: Nếu A’, B’, C’ là ba điểm lần lượt nằm trên các cạnh SA, SB, SC của hình chóp tam giác S. ABC. Khi đó:

III. Các dạng toán về hình chóp thường gặp

Phương pháp chung: tính diện tích đáy, các định chiều cao rồi áp dụng công thức \(V=\frac{1}{3}.S.h\)

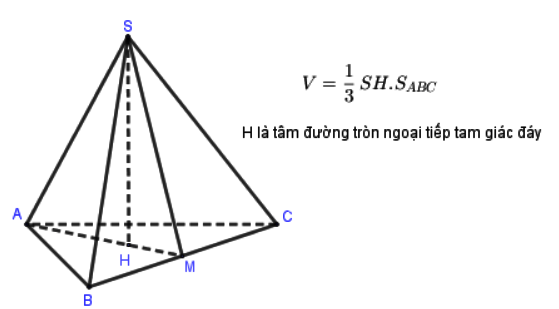
Dạng 1: Tính thể tích khối chóp đều

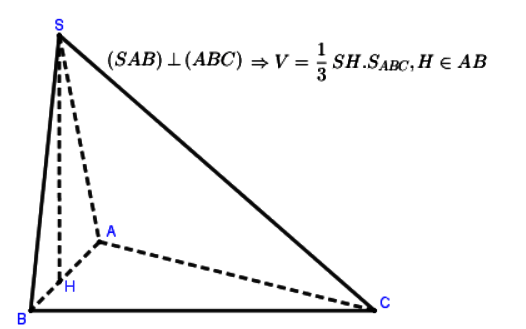
Dạng 2: Tính thể tích khối chóp có mặt bên vuông góc với đáy

Dạng 3: Tính thể tích hình chóp có cạnh bên vuông góc với đáy

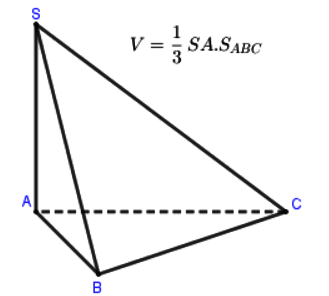
Dạng 4: Tính tỉ số thể tích của khối chóp

- Để tính tỉ số thể tích hai phần của một khối đa diện (H) được phân chia bởi một mặt phẳng (P) ta lựa chọn một trong hai cách:

Cách 1: Ta thực hiện theo các bước:

Bước 1: Dựng thiết diện tạo bởi (P) và (H) chai (H) thành hai hình (H’) và (H’’)

Bước 2: Dùng phương pháp tính thể tích đã biết để tính các thể tích V, V’ của hai hình (H’) và (H’’)

Bước 3: Tính tỉ số V/V’

Cách 2: Sử dụng kết quả:

Trên ba tia không đồng phẳng Sx, Sy, Sz lấy lần lượt các cặp điểm A và A’, B và B’, C và C’ khi đó ta luôn có: \(\frac{{{V}_{S.ABC}}}{{{V}_{S.A'B'C'}}}=\frac{SA}{SA'}.\frac{SB}{SB'}.\frac{SC}{SC'}\)

IV. Ví dụ thể tích khối chóp

Bài 1: Cho hình chóp tứ giác đều SABCD có các mặt bên là những tam giác đều, AB=8m, O là trung điểm của AC. Hình chóp SABCD có mấy cạnh? Độ dài SO là bao nhiêu?

Giải:

Hình chóp SABCD là hình chóp tứ giác nên có 8 cạnh.

Hình chóp SABCD đều nên đáy ABCD là hình vuông và tam giác OAB vuông cân tại O.

Áp dụng định lí Py-ta-go vào tam giác vuông OAB có

AB² = OB²+ OB²→ AB² = 2OA²

OA=\(\sqrt{\frac{AB^2}{2}}=\sqrt{\frac{8^2}{2}}=\sqrt{32}\)

Hình chóp có các mặt bên là tam giác đều nên tam giác SAB là tam giác đều. Do đó:

SA = AB = 8m

Ta có SO vuông góc với OA nên tam giác SOA vuông tại O. Áp dụng định lí Py-ta-go ta có:

SB² = OS² + OA²

\(SO=\sqrt{SA^2-OA^2}=\sqrt{8^2-32}=\sqrt{32}\)

V. Bài tập thể tích khối chóp

Câu 1. Cho khối tứ diện đều ABCD cạnh bằng a, M là trung điểm BC. Thể tích V của khối chóp M . A BC bằng bao nhiêu?

\(A. V=\frac{\sqrt{3} a^3}{24}.\)

\(B. V=\frac{a^3}{2}.\)

\(C. V=\frac{\sqrt{2} a^3}{12}.\)

\(D. V=\frac{\sqrt{2} a^3}{24}.\)

Câu 2. Cho hình chóp đều \(S \cdot ABCD\) có cạnh đáy bằng a và cạnh bên tạo với đáy một góc \(60^{\circ}\). Thể tích của hình chóp đểu đó là:

\(A. \frac{a^3 \sqrt{6}}{6}.\)

\(B. \frac{a^3 \sqrt{3}}{6}.\)

\(C. \frac{a^3 \sqrt{3}}{2}.\)

\(D. \frac{a^3 \sqrt{6}}{2}.\)

Câu 3. Thể tích hình tứ diện đều có cạnh bằng a là:

\(A. \frac{a^3 \sqrt{2}}{3}.\)

\(B. \frac{a^3 \sqrt{2}}{12}.\)

\(C. \frac{a^3 \sqrt{2}}{6}.\)

\(D. \frac{5 a^3 \sqrt{2}}{12}.\)

Câu 4.Cho khối chóp tứ giác đều có cạnh đáy bằng a, cạnh bên gấp hai lần cạnh đáy. Tính thể tích V của khối chóp tứ giác đã cho.

\(A. \frac{\sqrt{2} a^3}{2}.\)

\(B. \frac{\sqrt{2} a^3}{6}.\)

\(C. \frac{\sqrt{14} a^3}{6}.\)

\(D. \frac{\sqrt{14} a^3}{2}.\)

Câu 5. Cho hình chóp tứ giác đều có cạnh đáy bằng a và cạnh bên bằng \(a \sqrt{3}\). Tính thể tích V của khối chóp đó theo a.

\(A. V=\frac{a^3 \sqrt{3}}{3}.\)

\(B. V=\frac{a^3}{2}\).

\(C. V=\frac{a^3 \sqrt{2}}{3}.\)

\(D. V=\frac{a^3 \sqrt{10}}{6}.\)

Câu 6. Cho hình chóp tứ giác đều có tất cả các cạnh bằng nhau, đường cao của một mặt bên là \(a \sqrt{3}\). Thể tích V của khối chóp đó là:

\(A. V=\frac{\sqrt{2}}{6} a^3.\)

\(B. V=\frac{\sqrt{2}}{9} a^3.\)

\(C. V=\frac{2 \sqrt{2}}{3} a^3.\)

\(D. V=\frac{4 \sqrt{2}}{3} a^3.\)

Câu 7. Cho tứ diện đều ABCD cạnh bằng \(\sqrt{2} a\). Tính thể tích của khối tứ diện đó.

\(A. V=\frac{a^3 \sqrt{2}}{12}.\)

\(B. V=\frac{a^3 \sqrt{3}}{6}.\)

\(C. V=\frac{a^3}{3}\)

\(D. V=\frac{a^3 \sqrt{2}}{6}.\)

Câu 8. Cho hình chóp đều S.ABCD có cạnh đáy bằng 2 a, khoảng cách giữa hai đường thẳng S A và C D bằng \(a \sqrt{3}\). Thể tích khối chóp đều S.ABCD bằng?

\(A. 4 a^3 \sqrt{3}.\)

\(B.a^3\sqrt{3}.\)

\(C. \frac{4 a^3 \sqrt{3}}{3}.\)

\(D. \frac{a^3 \sqrt{3}}{3}.\)

Câu 9. Cho khối chóp đều S.ABC có cạnh bên bằng a và các mặt bên hợp với đáy một góc \(45^{\circ}\). Tính thể tích của khối chóp S.ABC theo a..

\(A. \frac{a^3 \sqrt{15}}{25}.\)

\(B. \frac{a^3 \sqrt{5}}{25}.\)

\(C. \frac{a^3}{3}.\)

\(D. \frac{a^3 \sqrt{15}}{5}.\)

Câu 10: Cho khối chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Biết S A vuông góc với (ABCD) và S A=a \sqrt{3}. Thể tích của khối chóp S . ABCD là:

Câu 11: Cho hình chóp tứ giác  SABCD có đáy là hình vuông cạnh a, S A vuông góc với mặt phẳng đáy và SA=2 a. Thể tích khối chóp S.ABCD bằng

Câu 12: Cho hình chóp S . ABCD có đáy ABCD là hình chữ nhật A B=a, B C=2 a, cạnh bên S A vuông góc với đáy và \(S A=a \sqrt{2}.\) Tính thể tích khối chóp S . ABCD.

Câu 13: Cho hình chóp S . ABCD có đáy ABCD là hình vuông cạnh a. Cạnh bên S A vuông góc với đáy và có độ dài bằng 2 a. Thể tích khối tứ diện S .BCD là:

Câu 14: Cho hình chóp S . ABCD có đáy ABCD là hình vuông tâm O cạnh 2 a. Biết S A vuông góc với mặt phẳng đáy và \(S A=a \sqrt{2}.\) Tính thể tích khối chóp S . A B O.