Phân dạng câu hỏi và bài tập trong đề thi THPT Quốc gia môn Toán Ôn thi THPT Quốc gia môn Toán
Các dạng toán thường gặp trong đề thi THPT Quốc gia 2023 giúp các em học sinh làm quen với các dạng bài hay gặp trong đề thi, thử sức với các câu hỏi khó giành điểm 9 – 10 và có chiến lược thời gian làm bài thi phù hợp nhất.
Các dạng Toán thi THPT Quốc gia bao gồm các dạng bài tính đơn điệu của hàm số, cực trị của hàm số, giá trị lớn nhất, giá trị nhỏ nhất của hàm số ... . Tài liệu được biên soạn theo mức độ khó và nâng cao dần giúp những em lớp 12 rèn luyện tư duy, hệ thống kiến thức bao quát những dạng toán thường gặp. Ngoài ra các em xem thêm 40 đề ôn thi THPT Quốc gia môn Toán.
Các dạng Toán thường gặp trong đề thi THPT Quốc gia
1. Tính đơn điệu của hàm số
1.1 (Đề minh họa 2016). Hỏi hàm số![]() \(y=2 x^4+1\) đồng biến trên khoảng nào?
\(y=2 x^4+1\) đồng biến trên khoảng nào?
![]() \(A. (-\infty ; 0).\)
\(A. (-\infty ; 0).\)
![]() \(B. (0 ;+\infty).\)
\(B. (0 ;+\infty).\)
![]() \(C. \left(-\infty ;-\frac{1}{2}\right).\)
\(C. \left(-\infty ;-\frac{1}{2}\right).\)
![]() \(D. \left(-\frac{1}{2} ;+\infty\right).\)
\(D. \left(-\frac{1}{2} ;+\infty\right).\)
Lời giải
Ta có ![]() \(y^{\prime}=8 x^3 ; y^{\prime}=0 \Leftrightarrow x=0\). Bảng biến thiên
\(y^{\prime}=8 x^3 ; y^{\prime}=0 \Leftrightarrow x=0\). Bảng biến thiên
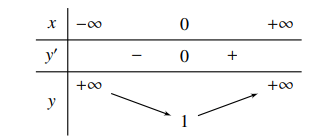
Từ bảng biến thiên ta thấy hàm số đồng biến trên ![]() \((0 ;+\infty)\). Chọn phương án B.
\((0 ;+\infty)\). Chọn phương án B.
1.2 (Đề chính thức 2017). Cho hàm số ![]() \(y=x^3+3 x+2\). Mệnh đề nào dưới đây đúng?
\(y=x^3+3 x+2\). Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ![]() \((-\infty ;+\infty).\)
\((-\infty ;+\infty).\)
B. Hàm số đồng biến trên khoảng ![]() \((-\infty ; 0)\) và nghịch biến trên khoảng
\((-\infty ; 0)\) và nghịch biến trên khoảng ![]() \((0 ;+\infty).\)
\((0 ;+\infty).\)
C. Hàm số nghịch biến trên khoảng![]() \((-\infty ; 0)\) và đồng biến trên khoảng
\((-\infty ; 0)\) và đồng biến trên khoảng ![]() \((0 ;+\infty).\)
\((0 ;+\infty).\)
D. Hàm số đồng biến trên khoảng ![]() \((-\infty ;+\infty).\)
\((-\infty ;+\infty).\)
Lời giải
Ta có ![]() \(y^{\prime}=3 x^2+3>0, \forall x \in(-\infty ;+\infty) n\) nên hàm số đồng biến trên
\(y^{\prime}=3 x^2+3>0, \forall x \in(-\infty ;+\infty) n\) nên hàm số đồng biến trên ![]() \((-\infty ;+\infty).\)
\((-\infty ;+\infty).\)
Chọn phương án D
1.3 (Đề tham khảo 2017). Cho hàm số ![]() \(y=\frac{x-2}{x+1}\). Mệnh đề nào dưới đây đúng?
\(y=\frac{x-2}{x+1}\). Mệnh đề nào dưới đây đúng?
A. Hàm số đồng biến trên khoảng (-\infty ;-1).
B. Hàm số nghịch biến trên khoảng![]() \((-1 ;+\infty).\)
\((-1 ;+\infty).\)
C. Hàm số đồng biến trên khoảng ![]() \((-\infty ;+\infty).\)
\((-\infty ;+\infty).\)
D. Hàm số nghịch biến trên khoảng ![]() \((-\infty ;-1).\)
\((-\infty ;-1).\)
Lời giải
Ta có ![]() \(y^{\prime}=\frac{3}{(x+1)^2}>0, \forall x \in \mathbb{R} \backslash\{-1\}\) nên hàm số đồng biến trên khoảng
\(y^{\prime}=\frac{3}{(x+1)^2}>0, \forall x \in \mathbb{R} \backslash\{-1\}\) nên hàm số đồng biến trên khoảng ![]() \((-\infty ;-1)\).
\((-\infty ;-1)\).
Chọn phương án A
1.4 (Đề thử nghiệm 2017). Cho hàm số ![]() \(y=x^3-2 x^2+x+1\). Mệnh đề nào dưới đây đúng?
\(y=x^3-2 x^2+x+1\). Mệnh đề nào dưới đây đúng?
A. Hàm số nghịch biến trên khoảng ![]() \(\left(\frac{1}{3} ; 1\right)\).
\(\left(\frac{1}{3} ; 1\right)\).
B. Hàm số nghịch biến trên khoảng ![]() \((1 ;+\infty).\)
\((1 ;+\infty).\)
A. Hàm số đồng biến trên khoảng ![]() \(\left(\frac{1}{3} ; 1\right)\).
\(\left(\frac{1}{3} ; 1\right)\).
D. Hàm số nghịch biến trên khoảng ![]() \(\left(-1 ;\frac{1}{3} \right)\).
\(\left(-1 ;\frac{1}{3} \right)\).
Lời giải ; Đáp án D
........
4. Điều kiện đơn điệu của hàm số ![]() \(y=a x^3+b x^2+c x+d\)
\(y=a x^3+b x^2+c x+d\)
1.19 (Đề tham khảo 2020). Có bao nhiêu giá trị nguyên của tham số m sao cho hàm số ![]() \(f(x)= \frac{1}{3} x^3+m x^2+4 x+3\) đồng biến trên R
\(f(x)= \frac{1}{3} x^3+m x^2+4 x+3\) đồng biến trên R
A. 3 .
B. 5 .
C. 2 .
D. 4 .
Lời giải
Ta có ![]() \(y^{\prime}=x^2+2 m x+4 ; \Delta^{\prime}=m^2-4.\)
\(y^{\prime}=x^2+2 m x+4 ; \Delta^{\prime}=m^2-4.\)
Hàm số đã cho đồng biến trên R khi và chỉ khi
![]() \(\left\{\begin{array} { l }
{ a > 0 } \\
{ \Delta ^ { \prime } \leqslant 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
1>0 \\
m^2-4 \leqslant 0
\end{array} \Leftrightarrow-2 \leqslant m \leqslant 2 .\right.\right.\)
\(\left\{\begin{array} { l }
{ a > 0 } \\
{ \Delta ^ { \prime } \leqslant 0 }
\end{array} \Leftrightarrow \left\{\begin{array}{l}
1>0 \\
m^2-4 \leqslant 0
\end{array} \Leftrightarrow-2 \leqslant m \leqslant 2 .\right.\right.\)
Vì ![]() \(m \in \mathbb{Z}\) nên
\(m \in \mathbb{Z}\) nên ![]() \(m \in\{-2,-1,0,1,2\}.\)
\(m \in\{-2,-1,0,1,2\}.\)
Vậy có 5 giá trị nguyên của m thỏa mãn yêu cầu bài toán. Chọn phương án B
1.20 (Đề chính thức 2017). Cho hàm số ![]() \(y=-x^3-m x^2+(4 m+9) x+5\) với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng
\(y=-x^3-m x^2+(4 m+9) x+5\) với m là tham số. Có bao nhiêu giá trị nguyên của m để hàm số nghịch biến trên khoảng ![]() \((-\infty ;+\infty) ?\)
\((-\infty ;+\infty) ?\)
A. 7 .
B. 4 .
C. 6 .
D. 5 .
Lời giải
Ta có ![]() \(y^{\prime}=-3 x^2-2 m x+4 m+9 ; \Delta^{\prime}=m^2+3(4 m+9)=m^2+12 m+27.\)
\(y^{\prime}=-3 x^2-2 m x+4 m+9 ; \Delta^{\prime}=m^2+3(4 m+9)=m^2+12 m+27.\)
Hàm số nghịch biến trên ![]() \((-\infty ;+\infty)\) khi và chỉ khi
\((-\infty ;+\infty)\) khi và chỉ khi ![]() \(\Delta^{\prime} \leqslant 0 \Leftrightarrow m^2+12 m+27 \leqslant 0 \Leftrightarrow-9 \leqslant m \leqslant-3.\)
\(\Delta^{\prime} \leqslant 0 \Leftrightarrow m^2+12 m+27 \leqslant 0 \Leftrightarrow-9 \leqslant m \leqslant-3.\)
Suy ra có 7 giá trị nguyên của m để hàm số nghịch biến trên![]() \((-\infty ;+\infty).\)
\((-\infty ;+\infty).\)
Chọn phương án A
1.21 (Đề tham khảo 2017). Hỏi có bao nhiêu số nguyên m để hàm số ![]() \(y=\left(m^2-1\right) x^3+(m-1) x^2- x+4\) nghịch biến trên khoảng
\(y=\left(m^2-1\right) x^3+(m-1) x^2- x+4\) nghịch biến trên khoảng ![]() \((-\infty ;+\infty) ?\)
\((-\infty ;+\infty) ?\)
A. 3 .
B. 2 .
C. 1 .
D. 0 .
Lời giải.
TH1: m=1 ta có y=-x+4 nên nghịch biến trên ![]() \((-\infty ;+\infty)\) (thỏa mãn ycbt).
\((-\infty ;+\infty)\) (thỏa mãn ycbt).
TH2: m=-1 ta có ![]() \(y=-2 x^2-x+4\) có đồ thị là parabol nên không thể nghịch biến trên
\(y=-2 x^2-x+4\) có đồ thị là parabol nên không thể nghịch biến trên ![]() \((-\infty ;+\infty)\) (không thỏa mãn ycbt).
\((-\infty ;+\infty)\) (không thỏa mãn ycbt).
TH3:![]() \(m \neq \pm 1 ta có y^{\prime}=3\left(m^2-1\right) x^2+2(m-1) x-1\). Do đó nếu hàm số nghịch biến trên
\(m \neq \pm 1 ta có y^{\prime}=3\left(m^2-1\right) x^2+2(m-1) x-1\). Do đó nếu hàm số nghịch biến trên ![]() \((-\infty ;+\infty) thì m^2-1<0\). Vì
\((-\infty ;+\infty) thì m^2-1<0\). Vì ![]() \(m \in \mathbb{Z}\) nên m=0. Với m=0 ta có
\(m \in \mathbb{Z}\) nên m=0. Với m=0 ta có ![]() \(y^{\prime}=-3 x^2-2 x-1\) có
\(y^{\prime}=-3 x^2-2 x-1\) có ![]() \(\Delta^{\prime}=1-3=-2<0\) nên hàm số nghịch biến trên
\(\Delta^{\prime}=1-3=-2<0\) nên hàm số nghịch biến trên ![]() \((-\infty ;+\infty)\) (thỏa mãn ycbt).
\((-\infty ;+\infty)\) (thỏa mãn ycbt).
Vậy có 2 giá trị nguyên của m thỏa mãn yêu cầu bài toán.
Chọn phương án B
..................
Tải file tài liệu để xem thêm Các dạng Toán thường gặp trong kỳ thi THPTQG
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Đáp án cuộc thi Giao lưu tìm hiểu An toàn giao thông cho giáo viên năm 2022 - 2023
-

Văn mẫu lớp 12: Nghị luận xã hội về sự thành công trong cuộc sống
-

Văn mẫu lớp 12: Nghị luận xã hội cách nuôi dưỡng vẻ đẹp tâm hồn
-

Soạn bài Tự đánh giá: Gói thuốc lá Cánh diều
-

Đề cương ôn tập học kì 2 môn Lịch sử - Địa lí lớp 5 năm 2024 - 2025 (Sách mới)
-

Bộ đề thi học kì 2 môn Hoạt động trải nghiệm hướng nghiệp 7 sách Kết nối tri thức với cuộc sống
-

Bài thu hoạch bồi dưỡng kiến thức quốc phòng an ninh đối tượng 3
-

Thuyết minh về trò chơi dân gian ô ăn quan (Dàn ý + 12 mẫu)
-

Viết bài luận về bản thân để tham gia câu lạc bộ tình nguyện
-

Phân tích nhân vật mẹ Lê trong Nhà mẹ Lê
Mới nhất trong tuần
-

Đáp án đề thi môn Toán THPT Quốc gia 2025 của Bộ GD&ĐT
50.000+ -
Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THCS&THPT Lê Lợi, Bình Thuận
5.000+ -

Bộ đề ôn thi THPT Quốc gia môn Toán năm 2023 (40 đề + đáp án)
100.000+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán Cụm trường THPT Chí Linh, Hải Dương
100+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THPT Lê Quảng Chí, Hà Tĩnh
100+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THPT Chuyên Lê Quý Đôn, Bình Định
100+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THPT Nguyễn Bỉnh Khiêm, Hà Nội
1.000+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THPT Trưng Vương, Bình Định
100+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán liên trường THPT Quảng Nam
1.000+ -

Đề thi thử THPT Quốc gia năm 2025 môn Toán trường THPT Tân Phú, Hồ Chí Minh
1.000+






 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo