Eballsviet.com
Học tập Lớp 11 Toán 11

Lý thuyết và bài tập chuyên đề giới hạn Tổng hợp lý thuyết và bài tập chuyên đề giới hạn

Giới thiệu Tải về Bình luận

Lý thuyết và bài tập chuyên đề giới hạn là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 11 cùng tham khảo.

Tài liệu gồm 75 trang tóm tắt lý thuyết chuyên đề giới hạn và tuyển chọn bài tập tự luận, trắc nghiệm giới hạn dãy số, giới hạn hàm số và hàm số liên tục có đáp án và lời giải chi tiết giúp học sinh học tốt chương trình Đại số và Giải tích 11 chương 4. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tại đây.

Tổng hợp lý thuyết và bài tập chuyên đề giới hạn

MỤC LỤC
PHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN
§1. GIỚI HẠN CỦA DÃY SỐ 01 - 14
§2. GIỚI HẠN CỦA HÀM SỐ 15 – 31
§3. HÀM SỐ LIÊN TỤC 32 – 40
ÔN TẬP CHƯƠNG IV 41 – 49
PHẦN II. TRẮC NGHIỆM
GIỚI HẠN CỦA DÃY SỐ 50 – 54
GIỚI HẠN CỦA HÀM SỐ 55 – 59
HÀM SỐ LIÊN TỤC 60 – 62
ÔN TẬP CHƯƠNG IV. GIỚI HẠN 63 – 72
ĐÁP ÁN TRẮC NGHIỆM 73 – 74
Toán 11 GV. Lư Sĩ Pháp
1
BT. ĐS&GT 11 Chương IV. Giới hạn
CHƯƠNG IV.
GIỚI HẠN
PHẦN I. LÝ THUYẾT VÀ BÀI TẬP TỰ LUẬN
§1. GIỚI HẠN CỦA DÃY SỐ
A. KIẾN THỨC CẤN NẮM
1. Giới hạn hữu hạn của dãy số
n
n
u
lim 0
→+∞
=
khi và chỉ khi
n
u
có thể nhỏ hơn một số dương bé tùy ý, kể từ một số hạng nào đó trở
đi.
n n
n n
v a v a
lim lim ( ) 0
→+∞ →+∞
= ⇔ − =
Dãy số (u
n
) có giới hạn 0 khi và chỉ khi dãy số
(
n
u
có giới hạn 0
2. Giới hạn vô cực
n
n
ulim
→+∞
= +∞
khi và chỉ khi
n
u
có thể lớn hơn một số dương lớn tùy ý, kể từ một số hạng nào đó
trở đi. Kí hiệu:
n n
u hay u khi nlim
= +∞ → +∞ → +∞
Dãy số (
n
u
) được gọi là có giới hạn
−∞
khi
n
→ +∞
nếu
n
ulim( )
− = +∞
Nhận xét:
n n
n n
u ulim lim ( )
→+∞ →+∞
= +∞ ⇔ − = −∞
;
n n
n n
u ulim lim ( )
→+∞ →+∞
= −∞ ⇔ − = +∞
Lưu ý: Thay cho viết
n n
n n
u L ulim , lim
→+∞ →+∞
= = ±∞
, ta viết
n n
u a ulim ,lim
= = ±∞
3. Các giới hạn đặc biệt
a)
n
1
lim 0
=
;
k
n
1
lim 0
=
;
k
nlim
= +∞
, với k nguyên dương.
b)
n
q
lim 0
=
, nếu
q
1
<
;
n
q
lim
= +∞
nếu q > 1
c)
c c
lim
=
;
k
c
n
lim 0
=
, lim(c u
n
) = climu
n
, với c là hằng số,
k
*
∈
ℕ
d)
n
n
q
lim 0
=
nếu
q
1
>
4. Định lí về giới hạn hữu hạn
Định lí 1. Nếu
n
u L
lim
=
và
n
v M
lim
=
, thì:
n n n n
u v u v L M
lim( ) lim lim
+ = + = +
n n n n
u v u v L M
lim( ) lim lim
− = − = −
n n n n
u v u v L M
lim . lim .lim .
= =
n
c u c L
lim( . ) .
= ( với c là hằng số)
n
n
u
L
v M
lim = (nếu
M
0
≠
)
Định lí 2. Giả sử
n
u L
lim
=
Nếu
n
u
0
≥
với mọi n thì
L
0
≥
và
n
u L
lim =
n
u L
lim
=
và
n
u L
3
3
lim =
Nếu
n
ulim
= +∞
thì
n
u
1
lim 0
=
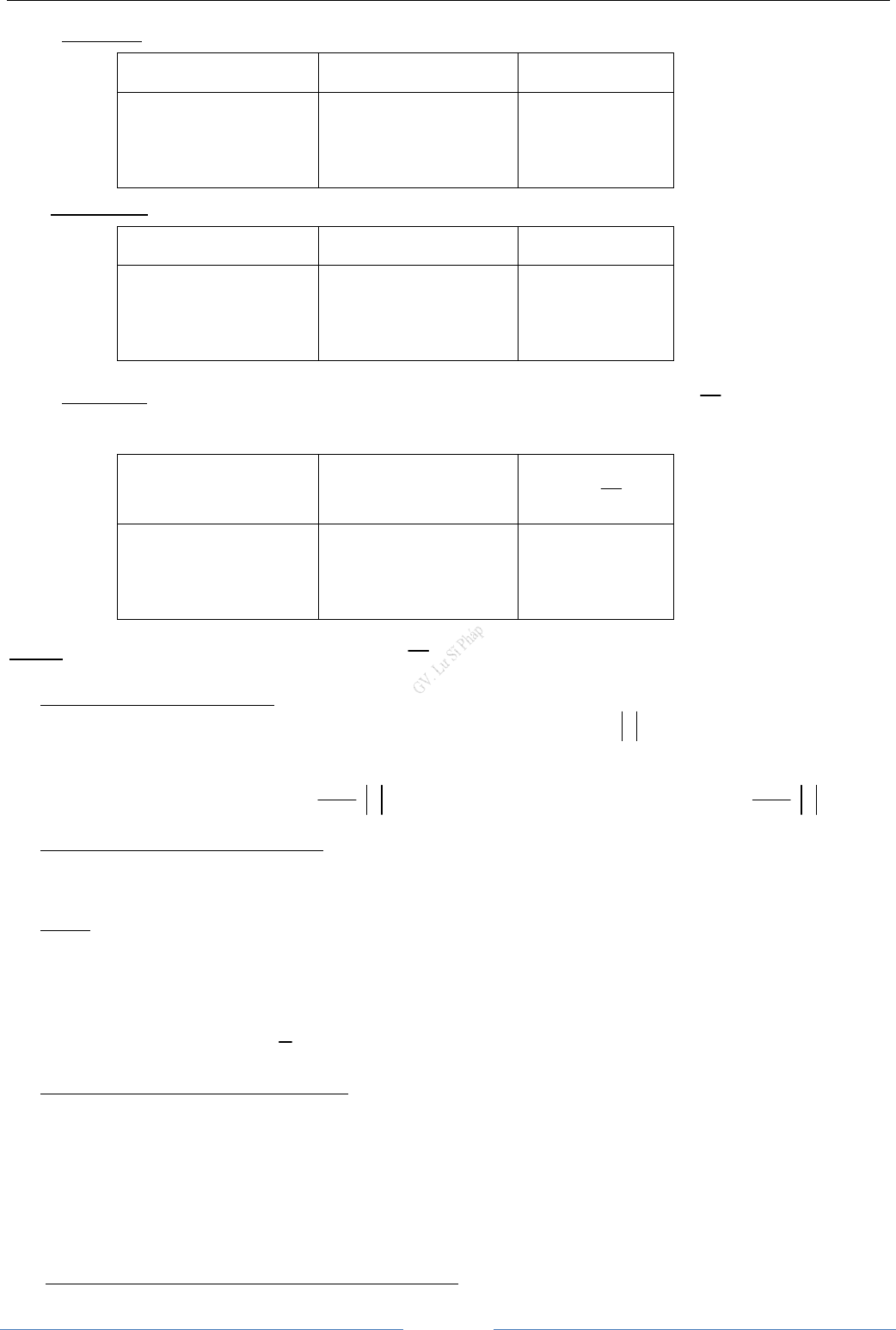
5. Một vài quy tắc tìm giới hạn vô cực
Toán 11 GV. Lư Sĩ Pháp
2
BT. ĐS&GT 11 Chương IV. Giới hạn
a) Quy tắc 1. Nếu
n
ulim
= ±∞
và
n
vlim
= ±∞
thì
(
n n
u v
lim
được cho trong bảng:
n
u
lim
n
v
lim
(
n n
u v
lim
+∞
+∞
−∞
−∞
+∞
−∞
+∞
−∞
+∞
−∞
−∞
+∞
b) Quy tắc 2. Nếu
n
ulim
= ±∞
và
n
v L
lim 0
= ≠
thì
(
n n
u v
lim
được cho trong bảng:
n
u
lim
Dấu của L
(
n n
u v
lim
+∞
+∞
−∞
−∞
+
−
+
−
+∞
−∞
−∞
+∞
c) Quy tắc 3. . Nếu
n
u L
lim 0
= ≠
và
n
v
lim 0
=
và
n
v
0
>
hoặc
n
v
0
<
thì
n
n
u
v
lim
được cho trong
bảng:
Dấu của L
Dấu của
n
v
n
n
u
v
lim
+
+
−
−
+
−
+
−
+∞
−∞
−∞
+∞
Chú ý . Nếu
n n
u L vlim 0,lim
= > = ±∞
thì
n
n
u
v
lim 0
=
6. Tổng cấp số nhân lùi vô hạn
Cấp số nhân lùi vô hạn là cấp số nhân có công bội q thỏa mãn q
1
<
Công thức tính tổng S của cấp số nhân lùi vô hạn (u
n
)
n
u
S u u u u q
q
1
1 2 3
... ... ; 1
1
= + + + + + = <
−
hay
n
u
S u u q u q u q q
q
2 1
1
1 1 1 1
... ... ; 1
1
−
= + + + + + = <
−
7. Định lí kẹp về giới hạn của dãy số
Cho ba dãy số (u
n
), (v
n
) ,(w
n
) và số thực L. Nếu
n n n
u v w
≤ ≤
với mọi n và lim u
n
= lim w
n
= L thì dãy
số (v
n
) có giới hạn và lim v
n
= L.
8. Lưu ý
a) Dãy số tăng và bị chặn trên thì có giới hạn
b) Dãy số giảm và bị chặn dưới thì có giới hạn
c) Nếu limu
n
= a thì limu
n + 1
= a
d) Số e:
n
n
e
n
1
lim 1
→+∞
= +
9. Phương pháp tìm giới hạn của dãy số
- Vận dụng nội dung định nghĩa
- Tìm giới hạn của một dãy số ta thường đưa về các giới hạn dạng đặc biệt và áp dụng các định lí về
giới hạn hoặc các định lí về giới hạn vô cực:
+ Nếu biểu thức có dạng phân thức mà mẫu và tử đều chứa các lũy thừa của n, thì chia tử và mẫu
cho n
k
, với k là số mũ cao nhất.
+ Nếu biểu thức có chứa n dưới dấu căn, thì có thể nhân tử số và mẫu số với cùng một biểu thức
liên hợp.
10. Phương pháp tính tổng của cấp số nhân lùi vô hạn
Liên kết tải về
Tìm thêm: Toán 11

Có thể bạn quan tâm

Xem thêm
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ

Mới nhất trong tuần