Toán 8 Bài 1: Định lí Pythagore Giải Toán 8 Chân trời sáng tạo trang 58, 59, 60, 61, 62

Toán lớp 8 tập 1 trang 58, 59, 60, 61, 62 Chân trời sáng tạo là tài liệu vô cùng hữu ích mà Eballsviet.com muốn giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 8 tham khảo.

Giải Toán 8 Chân trời sáng tạo Bài 1 Định lí Pythagore được biên soạn đầy đủ, chi tiết trả lời các câu hỏi phần bài tập cuối bài trang 61, 62. Qua đó giúp các bạn học sinh có thể so sánh với kết quả mình đã làm. Vậy sau đây là nội dung chi tiết Toán lớp 8 tập 1 chương III Bài 1 Định lí Pythagore Chân trời sáng tạo, mời các bạn cùng theo dõi tại đây.

Toán 8 Tập 1 trang 61, 62 Chân trời sáng tạo

Bài tập 1

Cho tam giác ABC vuông tại A.

a) Tính độ dài cạnh BC nếu biết AB = 7 cm, AC = 24 cm

b) Tính độ dài cạnh AB nếu biết AC = 2 cm, BC = $\sqrt{13}$ cm

c) Tính độ dài cạnh AC nếu biết BC = 25 cm, AB = 15 cm

Gợi ý đáp án

Áp dụng định lí Pythagore cho tam giác ABC vuông tại A ta có:

\(BC^{2}=AB^{2}+AC^{2}\)

a) suy ra \(BC^{2}= 7^{2}+24^{2}=625\). Vậy BC = 25 cm

b) suy ra \(AB^{2}=BC^{2}-AC^{2}=(\sqrt{13})^{2}-2^{2}=9\). Vậy AB = 3 cm

c) suy ra \(AC^{2}=Bc^{2}-AB^{2}=25^{2}-15^{2}=400\). Vậy AC = 20 cm

Bài tập 2

Tính độ cao của con diều so với mặt đất (Hình 11).

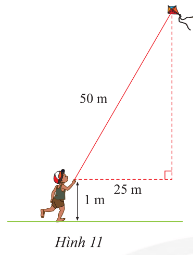
Gợi ý đáp án

Áp dụng định lí Pythagore cho tam giác ABC ta có: \(AB^{2}=AC^{2}+BC^{2}\) suy ra

\(AC^{2}=AB^{2}-BC^{2}=50^{2}-25^{2}=187\)

Do đó \(AC=25\sqrt{3}\) (m)

Độ cao của con diều so với mặt đất là \(25\sqrt{3}+1\approx 44.3\) (m)

Bài tập 3

Lần lượt tính độ dài các cạnh huyền a, b, c, d của các tam giác vuông trong hình 12. Hãy dự đoán kết quả của các cạnh huyền còn lại

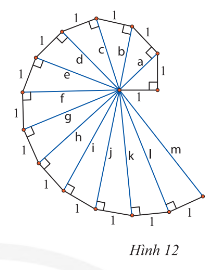
Gợi ý đáp án

Áp dụng định lí Pythagore cho tam giác vuông, ta có:

\(a^{2}=1^{2}+1^{2}=2.\) Mà a > 0 do đó: \(a =\sqrt{2}\)

\(b^{2}=1^{2}+a^{2}=1+2=3\). Mà b > 0 do đó \(b=\sqrt{3}\)

\(c^{2}=b^{2}+1=3+1=4\). Mà c > 0 do đó c = 2

\(d^{2}=c^{2}+1=4+1=5\). Mà d > 0 do đó: \(d=\sqrt{5}\)

Dự đoán độ dài các cạnh huyền còn lại lần lượt là:

\(e=\sqrt{6}, f=\sqrt{7},g=\sqrt{8},h=3,\)

\(i=\sqrt{10},j=\sqrt{11},k=\sqrt{12},l=\sqrt{13},m=\sqrt{14}\)

Bài tập 4

Chứng minh rằng tam giác ABC vuông trong các trường hợp sau:

a) AB = 8cm, AC = 15cm, BC = 17cm;

b) AB = 29cm, AC = 21cm, BC = 20cm;

c) AB = 12cm, AC = 37cm, BC = 35cm.

Gợi ý đáp án

a) Ta có: \(17^{2}=8^{2}+15^{2}\Rightarrow BC^{2}=AB^{2}+AC^{2}\). Vậy tam giác ABC vuông tại A

b) Ta có: \(29^{2}=21^{2}+20^{2}\Rightarrow AB^{2}=AC^{2}+BC^{2}\). Vậy tam giác ABC vuông tại C

c) Ta có: \(37^{2}=12^{2}+35^{2}\Rightarrow AC^{2}=AB^{2}+BC^{2}\). Vậy tam giác ABC vuông tại B

Bài tập 5

Cho biết thang của một xe cứu hỏa có chiều dài 13 cm, chân thang cách mặt đất 3m, và cách tường của tòa nhà 5 m. Tính chiều cao mà thang có thể vươn tới.

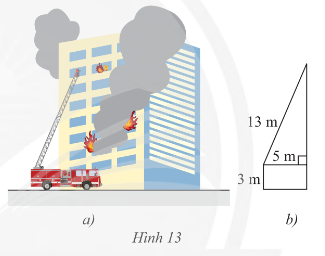
Gợi ý đáp án

Áp dụng định lí Pythagore ta có:

\(AB^{2}=AC^{2}+BC^{2}\Rightarrow AC^{2}=AB^{2}-BC^{2}=13^{2}-5^{2}=144\)

Do đó AC = 12 cm

Chiều cao mà thang có thể vươn tới là: 12 + 3=15 (m)

Bài tập 6

Một con thuyền đang neo ở một điểm cách chân tháp hải đăng 180 m. Cho biết tháp hải đăng cao 25 m. Hãy tính khoảng cách từ thuyền đến ngọn hải đăng

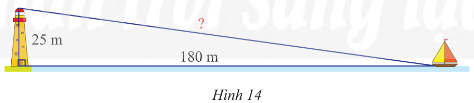
Gợi ý đáp án

Áp dụng định lí Pythagore ta có khoảng cách từ thuyền đến ngọn hải đăng là:

\(\sqrt{180^{2}+25^{2}}\approx 181.73\) (m)