Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số Giải Toán 12 Chân trời sáng tạo trang 6 → 13

Giải Toán 12 Bài 1: Tính đơn điệu và cực trị của hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Chân trời sáng tạo tập 1 trang 6, 7, 8, 9, 10, 11, 12, 13.

Giải bài tập Toán 12 Chân trời sáng tạo tập 1 Bài 1 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 1 Chương I: Ứng dụng đạo hàm để khảo sát hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 12 Chân trời sáng tạo Tập 1 trang 13

Bài 1

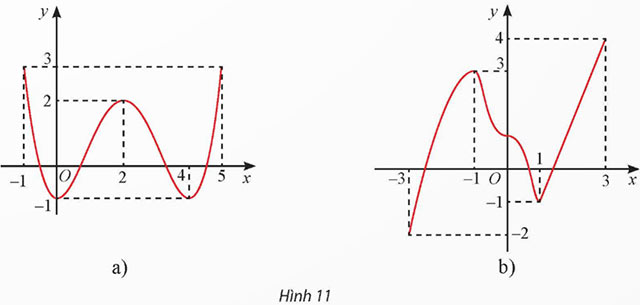
Tìm các khoảng đơn điệu và cực trị của các hàm số có đồ thị cho ở Hình 11.

Hướng dẫn giải:

a) Hình 11a:

Hàm số đồng biến trên các khoảng \(\left(-1; 2\right)\) và \((4;5)\); nghịch biến trên các khoảng \(\left(-1; 0\right)\) và \((2;4)\)

Hàm số đạt cực đại tại x = 2, giá trị cực đại là f(2) = 2; hàm số đạt cực tiểu tại x = 0 và x = 4, giá trị cực tiểu là f(0) = - 1 và f(4) = - 1.

b) Hình 11b:

Hàm số đồng biến trên các khoảng \(\left(-3; -1\right)\) và \((1;3)\); nghịch biến trên khoảng \(\left(-1; 1\right)\)

Hàm số đạt cực đại tại x = - 1, giá trị cực đại là f(- 1) = 3; hàm số đạt cực tiểu tại x = 1, giá trị cực tiểu là f(1) = - 1.

Bài 2

Xét tính đơn điệu và tìm điểm cực trị của các hàm số sau:

a) y = 4x³ + 3x² – 36x + 6;

b) \(y = \frac{x^{2}-2x-7 }{x-4}\)

Hướng dẫn giải:

a) y = 4x³ + 3x² – 36x + 6

Tập xác định của hàm số là ℝ.

Ta có: y' = 12x² + 6x - 36

y' = 0 \(\Leftrightarrow\) x = - 2 hoặc \(x=\frac{3}{2}\).

Lập bảng biến thiên của hàm số:

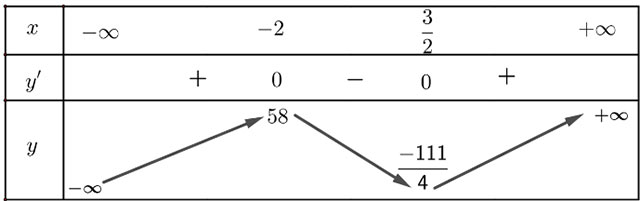
Hàm số đồng biến trên các khoảng \(\left(-∞;-2\right)\) và \(\left(\frac{3}{2} ;+∞\right)\), nghịch biến trên khoảng \(\left(-2;\frac{3}{2}\right)\)

Hàm số đạt cực đại tại x = - 2, giá trị cực đại là f(- 2) = 58; hàm số đạt cực tiểu tại \(x=\frac{3}{2}\), giá trị cực tiểu là \(f\left(\frac{3}{2}\right)=-\frac{111}{4}\)

b) \(y = \frac{x^{2}-2x-7 }{x-4}\)

Tập xác định của hàm số là ℝ \ {4}.

Ta có: \(y'=\frac{x^2-8x+15}{\left(x-4\right)^2}\)

y' = 0 \(\Leftrightarrow\) x = 4 hoặc x = 5.

Lập bảng biến thiên của hàm số:

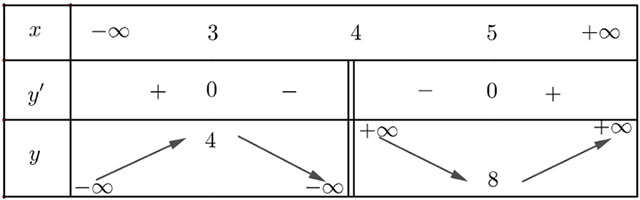
Hàm số đồng biến trên các khoảng \(\left(-∞;3\right)\) và \(\left(5 ;+∞\right)\), nghịch biến trên các khoảng \(\left(3;4\right)\) và \((4;5)\)

Hàm số đạt cực đại tại x = 3, giá trị cực đại là f(3) = 4; hàm số đạt cực tiểu tại x = 5, giá trị cực tiểu là f(5) = 8.

Bài 3

Tìm cực trị của các hàm số sau:

a) y = 2x³ + 3x² – 36x + 1;

b) \(y = \frac{x^{2} -8x+10}{x-2}\)

c) \(y = \sqrt{-x^{2} +4}\)

Hướng dẫn giải:

a) y = 2x³ + 3x² – 36x + 1

Tập xác định của hàm số là ℝ.

Ta có: y' = 6x² + 6x - 36

y' = 0 \(\Leftrightarrow\) x = - 3 hoặc x = 2.

Lập bảng biến thiên của hàm số:

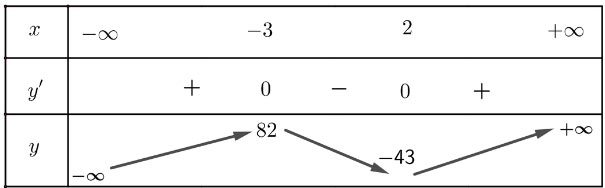
Hàm số đạt cực đại tại x = - 3, giá trị cực đại là f(- 3) = 82; hàm số đạt cực tiểu tại x = 2, giá trị cực tiểu là f(2) = - 43.

b) \(y = \frac{x^{2} -8x+10}{x-2}\)

Tập xác định của hàm số là ℝ \ {2}.

Ta có: \(y'=\frac{x^2-4x+6}{\left(x-2\right)^2} >0\) với mọi x khác 2.

Lập bảng biến thiên của hàm số:

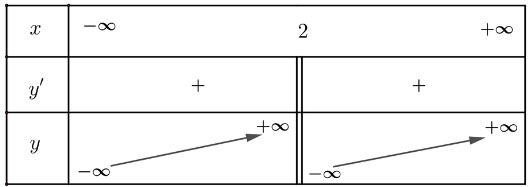
Hàm số không có cực trị.

c) \(y = \sqrt{-x^{2} +4}\)

Tập xác định của hàm số là [- 2; 2]

Ta có: \(y'=-\frac{x}{\sqrt{-x^2+4}}\); y' = 0 \(\Leftrightarrow\) x = 0

Lập bảng biến thiên của hàm số:

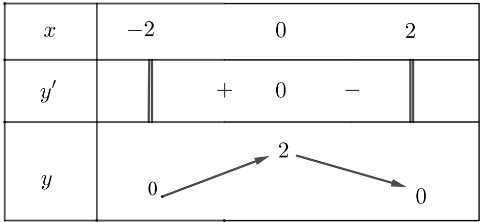
Hàm số đạt cực đại tại x = 0, giá trị cực đại là f(0) = 2.

Bài 4

Chứng minh rằng hàm số \(y = \frac{2x+1}{x-3}\) nghịch biến trên từng khoảng xác định của nó.

Hướng dẫn giải:

Xét hàm số \(y = \frac{2x+1}{x-3}\)

Tập xác định: ℝ \ {3}.

Ta có: \(y'=\frac{-7}{\left(x-3\right)^2} <0\) với mọi x khác 3.

Lập bảng biến thiên của hàm số:

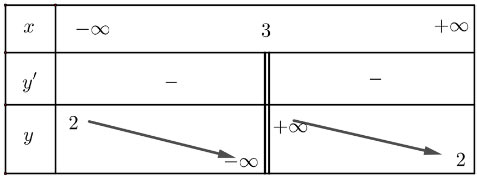
Vậy hàm số \(y = \frac{2x+1}{x-3}\) nghịch biến trên từng khoảng xác định của nó.

Bài 5

Kim ngạch xuất khẩu rau quả của Việt Nam trong các năm từ 2010 và 2017 có thể được tính xấp xỉ bằng công thức f(x) = 0,01x³ – 0,04x² + 0,25x + 0,44 (tỉ USD) với x là số năm tính từ 2010 đến 2017 (0 ≤ x ≤ 7).

a) Tính đạo hàm của hàm số y = f(x).

b) Chứng minh rằng kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Hướng dẫn giải:

a) Ta có: f'(x) = 0,03x² - 0,08x + 0,25

b) Tập xác định: ℝ

Ta có: f'(x) > 0 với mọi x thuộc ℝ nên f(x) đồng biến trên ℝ.

Do đó kim ngạch xuất khẩu rau quả của Việt Nam tăng liên tục trong các năm từ 2010 đến 2017.

Bài 6

Xét một chất điểm chuyển động dọc theo trục Ox. Tọa độ của chất điểm tại thời điểm t được xác định bởi hàm số x(t) = t³ – 6t² + 9t với t ≥ 0. Khi đó x'(t) là vận tốc của chất điểm tại thời điểm t, kí hiệu v(t); v'(t) là gia tốc chuyển động của chất điểm tại thời điểm t, kí hiệu a(t).

a) Tìm các hàm v(t) và a(t).

b) Trong khoảng thời gian nào vận tốc của chất điểm tăng, trong khoảng thời gian nào vận tốc của chất điểm giảm?

Hướng dẫn giải:

a) Ta có:

v(t) = x'(t) = 3t² - 12t + 9

a(t) = v'(t) = 6t - 12

b) a(t) = v'(t) ⇔ t = 2

Ta có a(t) < 0 với mọi t ∈ (0; 2) và a(t) > 0 với mọi t > 2

Vậy vận tốc của chất điểm giảm khi t ∈ (0; 2) và tăng khi t ∈ (2; +∞).

Bài 7

Đạo hàm f'(x) của hàm số y = f(x) có đồ thị như Hình 12. Xét tính đơn điệu và tìm điểm cực trị của hàm số y = f(x).

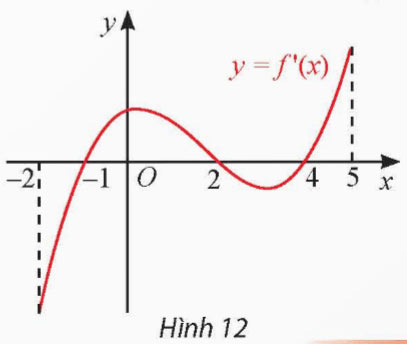
Hướng dẫn giải:

Ta có f'(x) > 0 trên các khoảng (-1; 2) và (4;5) nên f(x) đồng biến trên từng khoảng đó.

f'(x) < 0 trên các khoảng (-2; 1) và (2;4) nên f(x) nghịch biến trên từng khoảng đó.

Hàm số y = f(x):

Điểm cực đại tại x = 2 vì f'(x) đổi dấu dương sang âm khi x đi qua x = 2.

Điểm cực tiểu tại x = - 1 và x = 4 vì f'(x) đổi dấu âm sang dương khi x đi qua x = -1 và x= 4