Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số Giải Toán 12 Kết nối tri thức trang 20 → 25
Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Kết nối tri thức với cuộc sống tập 1 trang 20, 21, 22, 23, 24, 25.
Giải bài tập Toán 12 Kết nối tri thức tập 1 Bài 3 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 3 Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:
Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số
Giải Toán 12 Kết nối tri thức Tập 1 trang 25
Bài 1.16
Hình 1.26 là đồ thị của hàm số ![]() \(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
\(y = f\left( x \right) = \frac{{2{x^2}}}{{{x^2} - 1}}\)
Sử dụng đồ thị này, hãy:
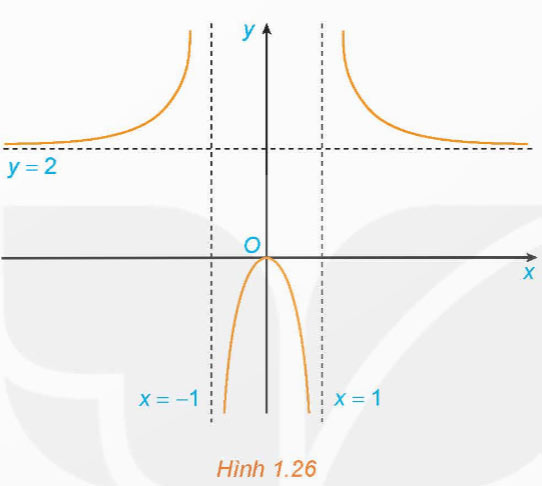
a) Viết kết quả của các giới hạn sau: ![]() \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right); \mathop {\lim }\limits_{x \to + \infty } f\left( x \right); \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right); \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right); \mathop {\lim }\limits_{x \to + \infty } f\left( x \right); \mathop {\lim }\limits_{x \to {1^ - }} f\left( x \right); \mathop {\lim }\limits_{x \to - {1^ + }} f\left( x \right)\)
b) Chỉ ra các tiệm cận của đồ thị hàm số đã cho.
Hướng dẫn giải:
a) Từ đồ thị ta có:
![]() \(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\);
\(\mathop {\lim }\limits_{x \to - \infty } f\left( x \right) = 2\); ![]() \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\)
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\)
![]() \(\mathop {\lim }\limits_{x \to 1^- } f\left( x \right) = -\infty\);
\(\mathop {\lim }\limits_{x \to 1^- } f\left( x \right) = -\infty\); ![]() \(\mathop {\lim }\limits_{x \to - 1^+ } f\left( x \right) = -\infty\)
\(\mathop {\lim }\limits_{x \to - 1^+ } f\left( x \right) = -\infty\)
b) Đồ thị hàm số có:
Tiệm cận ngang: y = 2
Tiệm cận đứng: x = - 1 và x = 1.
Bài 1.17
Đường thẳng x = 1 có phải là tiệm cận đứng của đồ thị hàm số ![]() \(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không?
\(y = \frac{{{x^2} + 2x - 3}}{{x - 1}}\) không?
Hướng dẫn giải:
Ta có: ![]() \(\lim_{x\rightarrow 1^+} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^+} \frac{{(x-1)(x+3)}}{{x - 1}}\)
\(\lim_{x\rightarrow 1^+} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^+} \frac{{(x-1)(x+3)}}{{x - 1}}\)
![]() \(= \lim_{x\rightarrow 1^+} (x+3)=4\)
\(= \lim_{x\rightarrow 1^+} (x+3)=4\)
![]() \(\lim_{x\rightarrow 1^-} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^-} \frac{{(x-1)(x+3)}}{{x - 1}}\)
\(\lim_{x\rightarrow 1^-} \frac{{{x^2} + 2x - 3}}{{x - 1}} = \lim_{x\rightarrow 1^-} \frac{{(x-1)(x+3)}}{{x - 1}}\)
![]() \(= \lim_{x\rightarrow 1^-} (x+3)=4\)
\(= \lim_{x\rightarrow 1^-} (x+3)=4\)
Vậy đường thẳng x = 1 không phải là tiệm cận đứng của đồ thị hàm số.
Bài 1.18
Tìm các tiệm cận của đồ thị các hàm số sau:
a) ![]() \(y = \frac{{3 - x}}{{2x + 1}}\);
\(y = \frac{{3 - x}}{{2x + 1}}\);
b) ![]() \(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).
\(y = \frac{{2{x^2} + x - 1}}{{x + 2}}\).
Hướng dẫn giải:
a) ![]() \(y = f(x)= \frac{{3 - x}}{{2x + 1}}\)
\(y = f(x)= \frac{{3 - x}}{{2x + 1}}\)
Ta có: ![]() \(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{3 - x}}{{2x + 1}} =-\frac{1}{2}\).
\(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{3 - x}}{{2x + 1}} =-\frac{1}{2}\).
Tương tự ![]() \(\lim_{x\rightarrow - \infty} f(x) =-\frac{1}{2}\)
\(\lim_{x\rightarrow - \infty} f(x) =-\frac{1}{2}\)
Vậy đồ thị hàm số f(x) có tiệm cận ngang là đường thẳng ![]() \(y=-\frac{1}{2}\).
\(y=-\frac{1}{2}\).
 \(\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+} \frac{{3 - x}}{{2x + 1}} = + \infty\).
\(\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^+} \frac{{3 - x}}{{2x + 1}} = + \infty\).
Tương tự ![]() \(\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^- } f(x) = - \infty\)
\(\lim_{x\rightarrow \left ( - \frac{1}{2}\right ) ^- } f(x) = - \infty\)
Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng ![]() \(x=-\frac{1}{2}\).
\(x=-\frac{1}{2}\).
b) Ta có:
* ![]() \(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty\).
\(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty\).
Tương tự ![]() \(\lim_{x\rightarrow - \infty} f(x) =-\infty\)
\(\lim_{x\rightarrow - \infty} f(x) =-\infty\)
Vậy hàm số không có tiệm cận ngang.
* ![]() \(\lim_{x\rightarrow \left ( - 2\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - 2\right ) ^+} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty\)
\(\lim_{x\rightarrow \left ( - 2\right ) ^+ } f(x) =\lim_{x\rightarrow \left ( - 2\right ) ^+} \frac{{2{x^2} + x - 1}}{{x + 2}} = + \infty\)
Tương tự ![]() \(\lim_{x\rightarrow \left ( - 2\right ) ^- } f(x) = - \infty\)
\(\lim_{x\rightarrow \left ( - 2\right ) ^- } f(x) = - \infty\)
Vậy đồ thị hàm số f(x) có tiệm cận đứng là đường thẳng x = - 2.
* ![]() \(f(x) = \frac{{2{x^2} + x - 1}}{{x + 2}} =(2x-3)+\frac{5}{x+2}\)
\(f(x) = \frac{{2{x^2} + x - 1}}{{x + 2}} =(2x-3)+\frac{5}{x+2}\)
![]() \(\lim_{x\rightarrow + \infty} [f(x) - (2x - 3)] =\lim_{x\rightarrow + \infty} \frac{5}{x+2} =0\).
\(\lim_{x\rightarrow + \infty} [f(x) - (2x - 3)] =\lim_{x\rightarrow + \infty} \frac{5}{x+2} =0\).
Vậy đồ thị hàm số f(x) có tiệm cận xiên là đường thẳng y = 2x - 3.
Bài 1.19
Một công ty sản xuất đồ gia dụng ước tính chi phí để sản xuất x (sản phẩm) là ![]() \(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó,
\(C\left( x \right) = 2x + 50\) (triệu đồng). Khi đó, ![]() \(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và
\(f\left( x \right) = \frac{{C\left( x \right)}}{x}\) là chi phí sản xuất trung bình cho mỗi sản phẩm. Chứng tỏ rằng hàm số f(x) giảm và ![]() \(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì?
\(\mathop {\lim }\limits_{x \to + \infty } f\left( x \right) = 2\). Tính chất này nói lên điều gì?
Hướng dẫn giải:
Hàm số ![]() \(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x+50}}{x}\)
\(f\left( x \right) = \frac{{C\left( x \right)}}{x} = \frac{{2x+50}}{x}\)
Ta có: ![]() \(f'\left(x\right)=-\frac{50}{x^2}\) < 0 với mọi x khác 0. Do đó hàm số f(x) giảm.
\(f'\left(x\right)=-\frac{50}{x^2}\) < 0 với mọi x khác 0. Do đó hàm số f(x) giảm.
![]() \(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2x+50}}{{x }} = 2\)
\(\lim_{x\rightarrow + \infty} f(x) =\lim_{x\rightarrow + \infty} \frac{{2x+50}}{{x }} = 2\)
Tính chất này cho biết chi phí sản xuất trung bình cho mỗi sản phẩm ít nhất là 2 triệu đồng (nhưng không bằng 2)
Bài 1.20
Một mảnh vườn hình chữ nhật có diện tích bằng 144m2. Biết độ dài một cạnh của mảnh vườn là x (m).
a) Viết biểu thức tính chu vi P(x) (mét) của mảnh vườn.
b) Tìm các tiệm cận của đồ thị hàm số P(x).
Hướng dẫn giải:
Độ dài cạnh còn lại của mảnh vườn là ![]() \(\frac{144}{x}\) (m)
\(\frac{144}{x}\) (m)
a) Biểu thức tính chu vi mảnh vườn là:
![]() \(P\left(x\right)=2\left(x+\frac{144}{x}\right) =2x+\frac{288}{x}\)
\(P\left(x\right)=2\left(x+\frac{144}{x}\right) =2x+\frac{288}{x}\)
b) Ta có:
* ![]() \(\lim_{x\rightarrow + \infty} P(x) =\lim_{x\rightarrow + \infty} \left ( 2x+\frac{288}{x} \right ) = + \infty\)
\(\lim_{x\rightarrow + \infty} P(x) =\lim_{x\rightarrow + \infty} \left ( 2x+\frac{288}{x} \right ) = + \infty\)
![]() \(\lim_{x\rightarrow - \infty} P(x) = - \infty\)
\(\lim_{x\rightarrow - \infty} P(x) = - \infty\)
Vậy hàm số không có tiệm cận ngang.
* ![]() \(\lim_{x\rightarrow 0 ^+ } P(x) =\lim_{x\rightarrow 0^+} \left ( 2x+\frac{288}{x} \right ) = + \infty\)
\(\lim_{x\rightarrow 0 ^+ } P(x) =\lim_{x\rightarrow 0^+} \left ( 2x+\frac{288}{x} \right ) = + \infty\)
Tương tự ![]() \(\lim_{x\rightarrow 0 ^+ } P(x) = - \infty\)
\(\lim_{x\rightarrow 0 ^+ } P(x) = - \infty\)
Vậy hàm số P(x) có tiệm cận đứng là đường thẳng x = 0.
* ![]() \(\lim_{x\rightarrow + \infty} [P(x) - (2x)] =\lim_{x\rightarrow + \infty} \frac{288}{x} =0\)
\(\lim_{x\rightarrow + \infty} [P(x) - (2x)] =\lim_{x\rightarrow + \infty} \frac{288}{x} =0\)
Vậy đồ thị hàm số P(x) có tiệm cận xiên là đường thẳng y = 2x.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-
Văn mẫu lớp 8: Phân tích nhân vật Đôn Ki-hô-tê trong truyện Đánh nhau với cối xay gió
-

Bộ đề thi học kì 2 môn Giáo dục công dân 7 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Bộ đề thi học kì 2 môn Toán 5 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Văn mẫu lớp 7: Đoạn văn cảm nhận tình cảnh của người nông dân trong Sống chết mặc bay
-

Kể lại buổi lễ kỉ niệm ngày Nhà giáo Việt Nam (2 Dàn ý + 10 mẫu)
-

Văn mẫu lớp 8: Cảm nhận về cái kết của truyện Cô bé bán diêm
-

Văn mẫu lớp 12: Phân tích 9 câu đầu bài Đất Nước của Nguyễn Khoa Điềm
-

Bài thu hoạch cá nhân về kết quả học tập, quán triệt Nghị quyết XII
-

Văn mẫu lớp 12: Nghị luận về nỗi sợ hãi của con người (Dàn ý + 8 mẫu)
-

Dàn ý 8 câu đầu bài Tình cảnh lẻ loi của người chinh phụ (5 mẫu)
Mới nhất trong tuần
-

Toán 12 Bài tập cuối chương III
100+ -

Toán 12 Bài 10: Phương sai và độ lệch chuẩn
100+ -

Toán 12 Bài 9: Khoảng biến thiên và khoảng tứ phân vị
100+ -

Toán 12 Bài tập cuối chương II
100+ -

Toán 12 Bài 8: Biểu thức toạ độ của các phép toán vectơ
100+ -

Toán 12 Bài 7: Hệ trục tọa độ trong không gian
100+ -

Toán 12 Bài 6: Vectơ trong không gian
100+ -

Toán 12 Bài tập cuối chương I
100+ -

Toán 12 Bài 5: Ứng dụng đạo hàm để giải quyết một số vấn đề liên quan đến thực tiễn
100+ -

Toán 12 Bài 4: Khảo sát sự biến thiên và vẽ đồ thị của hàm số
100+







 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo