Eballsviet.com
Học tập Lớp 10 Toán 10 Chân trời sáng tạo

Toán 10 Bài 1: Dấu của tam thức bậc hai Giải SGK Toán 10 trang 9, 10 - Tập 2 sách Chân trời sáng tạo

Giới thiệu Tải về Bình luận

Giải bài tập Toán 10 Chân trời sáng tạo Bài 1 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần vận dụng và 8 bài tập trang 9, 10 được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Chân trời sáng tạo tập 2 trang 9, 10 hướng dẫn giải bài tập Dấu của tam thức bậc hai trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 trang 9, 10 Chân trời sáng tạo mời các bạn cùng theo dõi.

Toán 10 Bài 1: Dấu của tam thức bậc hai

Phần Vận dụng

 Xét dấu tam thức bậc hai h(x) = -0,006x 2 + 1,2x – 30 trong bài toán khởi động và cho biết ở khoảng cách nào tính từ đầu cầu O thì vòm cầu: cao hơn mặt cầu, thấp hơn mặt cầu. 

Gợi ý đáp án 

Ta có h(x) = -0,006x2 + 1,2x – 30 là tam thức bậc hai. h(x) có ∆ = 1,22 – 4.(-0,006).(-30) = 0,72 > 0. Do đó tam thức có hai nghiệm phân biệt là x1 ≈ 170,7 và x2 ≈ 29,3 và a = - 0,006 < 0.

Ta có bảng xét dấu f(x) như sau:

Từ bảng xét dấu ta thấy f(x) dương trong khoảng (29,3; 170,7) và âm trong hai khoảng (-∞; 29,3) và (170,7; +∞).

Kết hợp với điều kiện 0 ≤ x ≤ 200 thì f(x) dương khi x ∈ (29,3; 170,7) và f(x) âm khi x ∈ [0; 29,3) và (170,7; 200].

Vậy với giá trị của x ∈ (29,3; 170,7) thì vòm cầu cao hơn mặt cầu, với giá trị của x nằm trong hai khoảng (-∞; 29,3) và (170,7; +∞) thì vòm cầu thấp hơn mặt cầu.

Phần Bài tập

Bài 1 trang 9

Đa thức nào sau đây là tam thức bậc hai?

a. 4{{x}^{2}}+3x+1\(a. 4{{x}^{2}}+3x+1\)

b. {{x}^{3}}+3{{x}^{2}}-1\(b. {{x}^{3}}+3{{x}^{2}}-1\)

c. 2{{x}^{2}}+4x-1\(c. 2{{x}^{2}}+4x-1\)

Gợi ý đáp án

a.4{{x}^{2}}+3x+1\(4{{x}^{2}}+3x+1\) là tam thức bậc hai có a = 4; b = 3; c = 1

b. {{x}^{3}}+3{{x}^{2}}-1\({{x}^{3}}+3{{x}^{2}}-1\) không là tam thức bậc hai

c. 2{{x}^{2}}+4x-1\(2{{x}^{2}}+4x-1\) là tam thức bậc hai có a = 2; b = 4; c = -1

Bài 2 trang 9

Xác định giá trị của m để các đa thức sau là tam thức bậc hai.

a. (m+1){{x}^{2}}+2x+m\(a. (m+1){{x}^{2}}+2x+m\)

b. m{{x}^{3}}+2{{x}^{2}}-x+m\(b. m{{x}^{3}}+2{{x}^{2}}-x+m\)

c. -5{{x}^{2}}+2x-m+1\(c. -5{{x}^{2}}+2x-m+1\)

Gợi ý đáp án

Giá trị của m để các đa thức sau là tam thức bậc hai:

a. (m+1){{x}^{2}}+2x+m\((m+1){{x}^{2}}+2x+m\) là tam thức bậc hai khi m+1\ne 0\Leftrightarrow m\ne -1\(m+1\ne 0\Leftrightarrow m\ne -1\)

b. m{{x}^{3}}+2{{x}^{2}}-x+m\(m{{x}^{3}}+2{{x}^{2}}-x+m\) không là tam thức bậc hai.

c. -5{{x}^{2}}+2x-m+1\(-5{{x}^{2}}+2x-m+1\) là tam thức bậc hai với mọi m.

Bài 3 trang 10

Dựa vào đồ thị của các hàm số bậc hai sau đây, hãy lập bảng xét dấu của tam thức bậc hai tương ứng.

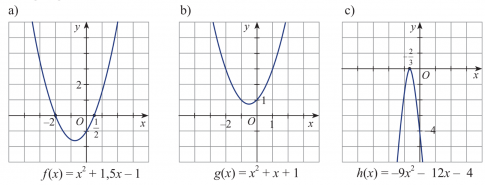
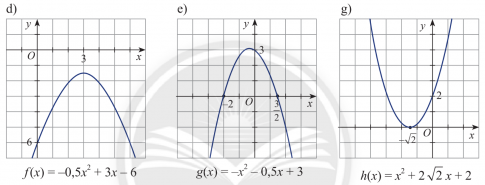
Gợi ý đáp án

a. f(x)={{x}^{2}}+1,5x-1 có \Delta =\frac{25}{4}>0\(f(x)={{x}^{2}}+1,5x-1 có \Delta =\frac{25}{4}>0\), hai nghiệm phân biệt là {{x}_{1}}=-2 ; {{x}_{2}}=\frac{1}{2} và a = 1 > 0\({{x}_{1}}=-2 ; {{x}_{2}}=\frac{1}{2} và a = 1 > 0\)

Ta có bảng xét dấu f(x) như sau:

Vậy f(x) dương trong hai khoảng \left( -\infty ;\frac{1}{2} \right)\(\left( -\infty ;\frac{1}{2} \right)\) và \left( -2;+\infty \right)\(\left( -2;+\infty \right)\) và âm trong khoảng \left( \frac{1}{2};-2 \right).\(\left( \frac{1}{2};-2 \right).\)

b. g(x)={{x}^{2}}+x+1\(g(x)={{x}^{2}}+x+1\) có \Delta =-3<0\(\Delta =-3<0\) và a =1 >0 . Vậy f(x) dương với mọi x\in \mathbb{R}\(x\in \mathbb{R}\)

c.h(x)=-9{{x}^{2}}-12x-4\(h(x)=-9{{x}^{2}}-12x-4\) có \Delta = 0,\(\Delta = 0,\) nghiệm kép là {{x}_{o}}=\frac{-2}{3}\({{x}_{o}}=\frac{-2}{3}\) và a =-9<0.

Vậy f(x) âm với mọi x\ne \frac{-2}{3}\(x\ne \frac{-2}{3}\)

d. f(x)=-0,5{{x}^{2}}+3x-6\(f(x)=-0,5{{x}^{2}}+3x-6\) có \Delta =-3<0\(\Delta =-3<0\) và a =-0,5 . Vậy f(x) âm với mọi x\in \mathbb{R}\(x\in \mathbb{R}\)

e. g(x)=-{{x}^{2}}-0,5x+3\(g(x)=-{{x}^{2}}-0,5x+3\) có \Delta =\frac{49}{4}>0\(\Delta =\frac{49}{4}>0\) , hai nghiệm phân biệt là {{x}_{1}}=-2 ; {{x}_{2}}=\frac{3}{2}\({{x}_{1}}=-2 ; {{x}_{2}}=\frac{3}{2}\) và a = -1 < 0

Ta có bảng xét dấu f(x) như sau:

Vậy f(x) dương trong hai khoảng \left( -\infty ;-2 \right)\(\left( -\infty ;-2 \right)\) và \left( \frac{3}{2};+\infty \right)\(\left( \frac{3}{2};+\infty \right)\) và âm trong khoảng \left( -2;\frac{3}{2} \right).\(\left( -2;\frac{3}{2} \right).\)

g. h(x)={{x}^{2}}+2\sqrt{2}x+2 có \Delta = 0\(h(x)={{x}^{2}}+2\sqrt{2}x+2 có \Delta = 0\), nghiệm kép là {{x}_{o}}=-\sqrt{2}\({{x}_{o}}=-\sqrt{2}\) và a = -9 < 0.

Vậy f(x) âm với mọi x\ne -\sqrt{2}\(x\ne -\sqrt{2}\)

Bài 4 trang 10

Xét dấu của tam thức bậc hai sau đây

a. f(x) = 2x^{2} + 4x + 2\(a. f(x) = 2x^{2} + 4x + 2\)

b. f(x) = -x^{2} + 2x + 21\(b. f(x) = -x^{2} + 2x + 21\)

c. f(x) = -2x^{2} + x - 2\(c. f(x) = -2x^{2} + x - 2\)

d. f(x) = -4x (x+3) - 9\(d. f(x) = -4x (x+3) - 9\)

e. f(x) = (2x+5) (x-3)

Gợi ý đáp án

a. \Delta = 4^{2} - 4.2.2 = 0\(\Delta = 4^{2} - 4.2.2 = 0\). Và đa thức có nghiệm x= \frac{-4}{2.2}=-1\(x= \frac{-4}{2.2}=-1\)

Mặt khác a= 2 > 0 nên f(x) luôn dương với mọi x khác -1

b.\Delta = 2^{2} - 4(-3).21 = 256 > 0\(\Delta = 2^{2} - 4(-3).21 = 256 > 0\) nên phương trình có hai nghiệm phân biệt : x= \frac{-2-\sqrt{256}}{2.(-3)} = 3; x = \frac{-7}{3}\(x= \frac{-2-\sqrt{256}}{2.(-3)} = 3; x = \frac{-7}{3}\) và a= -1 < 0 nên f(x) mang dấu âm khi x nằm trong khoảng (\frac{-7}{3}; 3)\((\frac{-7}{3}; 3)\) và mang dấu dương với mọi x nằm ngoài khoảng (\frac{-7}{3}; 3)\((\frac{-7}{3}; 3)\)

c.\Delta = (-2)^{2} - 4(-2)(-2)= -12< 0\(\Delta = (-2)^{2} - 4(-2)(-2)= -12< 0\) và a= -2 < 0 nên f(x) luôn âm với mọi x

d. f(x)= -4x^{2} - 12x -9\(d. f(x)= -4x^{2} - 12x -9\).

\Delta = (-12)^{2} - 4(-4)(-9) = 0\(\Delta = (-12)^{2} - 4(-4)(-9) = 0\) nên có nghiệm kép là x = -1,5 và a= -4

\Rightarrow f(x) mang dấu âm với mọi x khác -1,5

e. f(x) = 2x^{2} - x - 15.

\Delta = (-1)^{2} - 4.2.15= -119 < 0\(\Delta = (-1)^{2} - 4.2.15= -119 < 0\), và a= 2 > 0 nên f(x)  âm

Bài 5 trang 10

Độ cao ( tính bằng mét) của quả bóng so với vành rổ khi bóng di chuyển được x mét theo phương ngang được mô phỏng theo hàm số h(x) = -0,1x^{2} + x -1.\(h(x) = -0,1x^{2} + x -1.\)Trong các khoảng nào của x thì bóng nằm: cao hơn vành rổ, thấp hơn vành rổ, và ngang vành rổ. Làm tròn kết quả đến hàng phần mười.

Gợi ý đáp án

Hàm số h(x) có \Delta = 1^{2} -4(-0,1)(-1) = 0,6 >0\(\Delta = 1^{2} -4(-0,1)(-1) = 0,6 >0\) nên sẽ có hai nghiệm phân biệt : x_{1} = 9, x_{2} = 1. và a = -0,1<0\(x_{1} = 9, x_{2} = 1. và a = -0,1<0\)

Vây :

  • Bóng nằm cao hơn vành rổ khi bóng nằm trong khoảng (1;9)
  • Bóng nằm thấp hơn vành rổ khi bóng nằm trong khoảng (-\infty ; 1)\((-\infty ; 1)\) và ( 9; +\infty )\(( 9; +\infty )\)
  • Bóng nằm ngang vành rổ khi bóng ở độ cao 1m hoặc 9m

Bài 6 trang 10

Một khung dây thép hình chữ nhật có chiều dài 20cm và chiều rộng 15cm được uốn lại thành khung hình chữ nhật mới có kích thước (20 +x) và (15-x) cm. Với x nằm trong khoảng nào thì diện tích của khung sau khi uốn: tăng lên, không thay đổi, giảm đi.

Gợi ý đáp án

Diện tích của khung dây thép khi chưa uốn là : 20.15 = 300 (cm^{2}\(cm^{2}\))

Diện tích của khung dây thép khi đã uốn là : (20 + x). (15-x) = 300 - 5x - x^{2}\((20 + x). (15-x) = 300 - 5x - x^{2}\). Như vậy diện tích của khung sau khi uốn tùy thuộc vào giá trị của hàm số f(x) = 5x + x^{2}.\(f(x) = 5x + x^{2}.\)

Xét hàm số f(x) có \Delta = 5^{2} - 4.1.0 = 25 > 0 \Rightarrow\(\Delta = 5^{2} - 4.1.0 = 25 > 0 \Rightarrow\)có hai nghiệm phân biệt :

x_{1} = \frac{-5-\sqrt{25}}{2. 1}= -5; x_{2} = \frac{-5+\sqrt{25}}{2. 1}= 0\(x_{1} = \frac{-5-\sqrt{25}}{2. 1}= -5; x_{2} = \frac{-5+\sqrt{25}}{2. 1}= 0\) và có a = 1 > 0. Nên :

  • f(x) mang dấu dương khi x thuộc (-5;0) \Rightarrow\(\Rightarrow\) Diện tích khung hình sau khi uốn nhỏ hơn trước khi uốn (giảm đi )
  • f(x) mang dấu âm khi x thuộc (-\infty ; -5) và (0 ; +\infty ) \Rightarrow\((-\infty ; -5) và (0 ; +\infty ) \Rightarrow\) Diện tích khung hình sau khi uốn lớn hơn trước khi uốn (tăng lên )
  • f(x) = 0 khi x = 0 hoặc x = -5 \Rightarrow\(\Rightarrow\) Diện tích khung hình sau khi uốn và trước khi uốn là không thay đổi

Bài 7 trang 10

Chứng minh rằng với mọi số thực m ta luôn có : 9m^{2} + 2m > -3\(9m^{2} + 2m > -3\)

Xét hàm số f(m) = 9m^{2} + 2m + 3\(f(m) = 9m^{2} + 2m + 3\). Ta có \Delta = 2^{2}- 4.9.3 = -104 < 0\(\Delta = 2^{2}- 4.9.3 = -104 < 0\) và có a = 9 > 0. Nên f(m) > 0 với mọi m nghĩa là 9m^{2} + 2m > 3\(9m^{2} + 2m > 3\)

Bài 8 trang 10

Tìm giá trị của m để :

a. 2x^{2} + 3x + m + 1 > 0\(. 2x^{2} + 3x + m + 1 > 0\) với mọi x\epsilon \mathbb{R}\(x\epsilon \mathbb{R}\)

b. mx^{2} + 5x - 3 \leq 0\(mx^{2} + 5x - 3 \leq 0\) với mọi x\epsilon \mathbb{R}\(x\epsilon \mathbb{R}\)

Gợi ý đáp án

a. Hàm số 2x^{2} + 3x + m + 1\(2x^{2} + 3x + m + 1\) có\Delta = 3^{2} - 4.2(m+1) = 1- 8m\(\Delta = 3^{2} - 4.2(m+1) = 1- 8m\). và a= 2 > 0 nên:

Để 2x^{2} + 3x + m + 1 > 0\(2x^{2} + 3x + m + 1 > 0\) với mọi x\epsilon \mathbb{R}\(x\epsilon \mathbb{R}\) thì \Delta < 0 \Rightarrow 1 - 8m < 0 \Rightarrow m> \frac{1}{8}\(\Delta < 0 \Rightarrow 1 - 8m < 0 \Rightarrow m> \frac{1}{8}\)

b. Xét hàm số mx^{2} + 5x - 3\(mx^{2} + 5x - 3\) có : \Delta = 5^{2} - 4.m.(-3) = 25 + 12m\(\Delta = 5^{2} - 4.m.(-3) = 25 + 12m\)

Để mx^{2} + 5x - 3 \leq 0\(mx^{2} + 5x - 3 \leq 0\) với mọi x\epsilon \mathbb{R} thì :\(x\epsilon \mathbb{R} thì :\)

\Delta < 0\(\Delta < 0\) và m < 0 \Rightarrow m < \frac{-25}{12}\(m < 0 \Rightarrow m < \frac{-25}{12}\)

Lý thuyết Dấu của tam thức bậc hai

1. Tam thức bậc hai

Đa thức bậc hai f\left( x \right) = a{x^2} + bx + c\(f\left( x \right) = a{x^2} + bx + c\) với a, b, c là hệ số, a \ne 0\(a \ne 0\) và x là biến số được gọi là tam thức bậc hai.

* Cho tam thức bậc hai f\left( x \right) = a{x^2} + bx + c\(f\left( x \right) = a{x^2} + bx + c\) a \ne 0\(a \ne 0\). Khi thay x bằng giá trị x0 vào ƒ(x), ta được f\left( {{x_0}} \right) = a{x_0}^2 + b{x_0} + c\(f\left( {{x_0}} \right) = a{x_0}^2 + b{x_0} + c\), gọi là giá trị của tam thức bậc lai tại x0.

+ Nếu f\left( {{x_0}} \right) > 0\(f\left( {{x_0}} \right) > 0\) thì ta nói f(x) đương tại x0;

+ Nếu f\left( {{x_0}} \right) < 0\(f\left( {{x_0}} \right) < 0\) thì ta nói f(x) âm tại x0;

+ Nếu f(x) đương (âm) tại mọi điểm x thuộc một khoảng hoặc một đoạn thì ta nói f(x) dương (âm) trên khoảng hoặc đoạn đó.

* Cho tam thức bậc hai f\left( x \right) = a{x^2} + bx + c\(f\left( x \right) = a{x^2} + bx + c\) a \ne 0\(a \ne 0\). Khi đó

+ Nghiệm của phương trình bậc hai a{x^2} + bx + c\(a{x^2} + bx + c\) là nghiệm của f(x).

+ Biểu thức \Delta = {b^2} - 4{\rm{a}}c và \Delta \(\Delta = {b^2} - 4{\rm{a}}c và \Delta ' = {\left( {\frac{b}{2}} \right)^2} - ac\) lần lượt là biệt thức và biệt thức thu gọn của f(x).

Ví dụ: Biểu thức nào sau đây là tam thức bậc hai? Nếu là tam thức bậc hai, hãy xét đâu của nó tại x=2

\begin{array}{l} a)f(x) = - {x^2} + x + 3\\ b)g(x) = - 3x + \frac{{13}}{2} \end{array}\(\begin{array}{l} a)f(x) = - {x^2} + x + 3\\ b)g(x) = - 3x + \frac{{13}}{2} \end{array}\)

Giải

a) Biểu thức f(x) = - {x^2} + x + 3\(- {x^2} + x + 3\) là một tam thức bậc hai.

f(2) = - {2^2} + 2 + 3 = 1 > 0\(- {2^2} + 2 + 3 = 1 > 0\) nên f(x) đương tại x = 2.

b) Biểu thức g(x) = - 3x + \frac{{13}}{2}\(- 3x + \frac{{13}}{2}\) không phải lả một tam thức bậc hai

 

Chia sẻ bởi: 👨 Trịnh Thị Thanh
Liên kết tải về
Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 10
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Xem thêm
Tìm bài trong mục này
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ