Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 Giải SGK Toán 10 trang 65 - Tập 1 sách Chân trời sáng tạo

Tải về

Toán 10 Chân trời sáng tạo trang 65 giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các câu hỏi phần Thực hành và 7 bài tập được nhanh chóng và dễ dàng hơn.

Giải Toán 10 Chân trời sáng tạo trang 65 tập 1 hướng dẫn giải bài tập trong sách giáo khoa rất chi tiết. Hy vọng rằng tài liệu sẽ giúp các em học sinh học tốt môn Toán 10. Đồng thời các thầy cô giáo, bậc phụ huynh có thể sử dụng tài liệu để hướng dẫn các em khi tự học ở nhà được thuận tiện hơn. Vậy sau đây là trọn bộ tài liệu giải Toán 10 Chân trời sáng tạo trang 65 mời các bạn cùng theo dõi.

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 ⁰

Phần Thực hành Toán 10 Chân trời sáng tạo Bài 1

Thực hành 1

Tìm các giá trị lượng giác của góc 135 ⁰

Gợi ý đáp án

Hình vẽ minh họa:

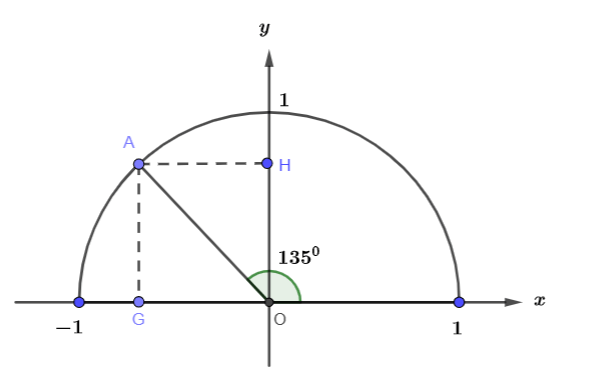
Lấy điểm A trên nửa đường tròn đơn vị sao cho $\widehat {xOA} = {135^{0}}$ $\widehat {xOA} = {135^{0}}$

Ta có:

$\widehat {yOA} = {180^0} - {135^0} = {45^0}$ $\widehat {yOA} = {180^0} - {135^0} = {45^0}$

Ta tính được tọa độ điểm A là $A = \left( {\frac{{ - \sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)$ $A = \left( {\frac{{ - \sqrt 2 }}{2};\frac{{\sqrt 2 }}{2}} \right)$

Vậy theo định nghĩa ta có:

$\sin {135^0} = \frac{{\sqrt 2 }}{2}$ $\sin {135^0} = \frac{{\sqrt 2 }}{2}$

$\cos{135^0} = -\frac{{\sqrt 2 }}{2}$ $\cos{135^0} = -\frac{{\sqrt 2 }}{2}$

$\tan {135^0} =- 1$ $\tan {135^0} =- 1$

$\cot {135^0} = -1$ $\cot {135^0} = -1$

Thực hành 2

Tính các giá trị lượng giác sin120 ⁰ ; cos150 ⁰ ; cot135 ⁰ .

Gợi ý đáp án

Thực hiện phép tính ta có kết quả như sau:

sin120⁰ = sin (180⁰ – 120⁰) = sin60⁰ = $\frac{{\sqrt 3 }}{2}$ $\frac{{\sqrt 3 }}{2}$

cos150⁰ = -cos(180⁰ – 150⁰) = -cos 30⁰ = $-\frac{{\sqrt 3 }}{2}$ $-\frac{{\sqrt 3 }}{2}$

cot135⁰ = - cot(180⁰– 135⁰) = -cot 45⁰ = -1

Bài tập Toán 10 trang 65 Chân trời sáng tạo

Bài 1 trang 65 Toán 10 Chân trời sáng tạo

Cho biết $\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1$ $\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1$. Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của

$E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.$ $E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.$

Gợi ý đáp án

Ta có:

$\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}$ $\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}$

$\Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.$ $\Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.$

Bài 2 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh các hệ thức sau:

$a) \sin {20^o} = \sin {160^o}$ $a) \sin {20^o} = \sin {160^o}$

$b) \cos {50^o} = - \cos {130^o}$ $b) \cos {50^o} = - \cos {130^o}$

Gợi ý đáp án

$\sin {20^o} = \sin \left( {{{180}^o} - {{160}^o}} \right) = \sin {160^o}$ $\sin {20^o} = \sin \left( {{{180}^o} - {{160}^o}} \right) = \sin {160^o}$

$\cos {50^o} = \cos \;({180^o} - {130^o}) = - \cos {130^o}$ $\cos {50^o} = \cos \;({180^o} - {130^o}) = - \cos {130^o}$

Bài 3 trang 65 Toán 10 Chân trời sáng tạo

Tìm góc $\alpha \;\;({0^o} \le \alpha \le {180^o})$ $\alpha \;\;({0^o} \le \alpha \le {180^o})$ trong mỗi trường hợp sau:

$a) \cos \alpha = - \frac{{\sqrt 2 }}{2}$ $a) \cos \alpha = - \frac{{\sqrt 2 }}{2}$

$b) \sin \alpha = 0$ $b) \sin \alpha = 0$

$c) \tan \alpha = 1$ $c) \tan \alpha = 1$

d) $\cot \alpha$ $\cot \alpha$ không xác định.

Gợi ý đáp án

a) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cos \alpha$ $\cos \alpha$ta có:

$\cos \alpha = \frac{{ - \sqrt 2 }}{2} với \alpha = {135^o}$ $\cos \alpha = \frac{{ - \sqrt 2 }}{2} với \alpha = {135^o}$

b) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\sin \alpha$ $\sin \alpha$ta có:

$\sin \alpha = 0 với \alpha = {0^o} và \alpha = {180^o}$ $\sin \alpha = 0 với \alpha = {0^o} và \alpha = {180^o}$

c) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\tan \alpha$ $\tan \alpha$ta có:

$\tan \alpha = 1 với \alpha = {45^o}$ $\tan \alpha = 1 với \alpha = {45^o}$

d) Sử dụng bảng giá trị lượng giác của các góc đặc biệt, hàng $\cot \alpha$ $\cot \alpha$ta có:

$\cot \alpha$ $\cot \alpha$không xác định với $\alpha = {0^o}$ $\alpha = {0^o}$

Bài 4 trang 65 Toán 10 Chân trời sáng tạo

Cho tam giác ABC. Chứng minh rằng:

$a) \sin A = \sin \;(B + C)$ $a) \sin A = \sin \;(B + C)$

$b) \cos A = - \cos \;(B + C)$ $b) \cos A = - \cos \;(B + C)$

Gợi ý đáp án

$\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A$ $\sin (B + C) = \sin \left( {{{180}^o} - A} \right) = \sin A$

Vậy $\sin A = \sin \;(B + C)$ $\sin A = \sin \;(B + C)$

$\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A$ $\cos (B + C) = \cos \left( {{{180}^o} - A} \right) = - \cos A$

Vậy $\cos A = - \cos \;(B + C)$ $\cos A = - \cos \;(B + C)$

Bài 5 trang 65 Toán 10 Chân trời sáng tạo

Chứng minh rằng với mọi góc $\alpha \;\;({0^o} \le \alpha \le {180^o}),$ $\alpha \;\;({0^o} \le \alpha \le {180^o}),$ ta đều có:

Gợi ý đáp án

$a) {\cos ^2}\alpha + {\sin ^2}\alpha = 1$ $a) {\cos ^2}\alpha + {\sin ^2}\alpha = 1$

Trên nửa đường tròn đơn vị, lấy điểm M sao cho $\widehat {xOM} = \alpha$ $\widehat {xOM} = \alpha$

Gọi H, K lần lượt là các hình chiếu vuông góc của M trên Ox, Oy.

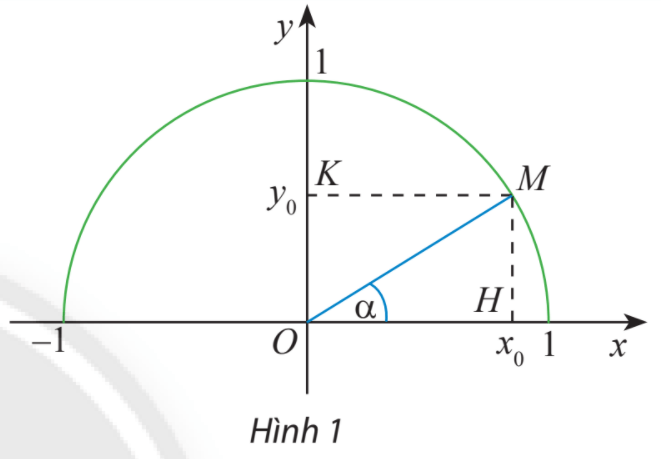
Ta có: tam giác vuông OHM vuông tại H và $\alpha = \widehat {xOM}$ $\alpha = \widehat {xOM}$

Do đó: $\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.$ $\sin \alpha = \frac{{MH}}{{OM}} = MH;\;\cos \alpha = \frac{{OH}}{{OM}} = OH.$

$\Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1$ $\Rightarrow {\cos ^2}\alpha + {\sin ^2}\alpha = O{H^2} + M{H^2} = O{M^2} = 1$

b) $\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})$ $\tan \alpha .\cot \alpha = 1\;({0^o} < \alpha < {180^o},\alpha \ne {90^o})$

Ta có:

$\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}$ $\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }}.\\ \Rightarrow \;\tan \alpha .\cot \alpha = \frac{{\sin \alpha }}{{\cos \alpha }}.\frac{{\cos \alpha }}{{\sin \alpha }} = 1\end{array}$

$c) 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})$ $c) 1 + {\tan ^2}\alpha = \frac{1}{{{{\cos }^2}\alpha }}\;(\alpha \ne {90^o})$

Với $\alpha \ne {90^o}$ $\alpha \ne {90^o}$ ta có:

$\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}$ $\begin{array}{l}\;\tan \alpha = \frac{{\sin \alpha }}{{\cos \alpha }};\;\\ \Rightarrow \;1 + {\tan ^2}\alpha = 1 + \frac{{{{\sin }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\cos }^2}\alpha }} = \frac{1}{{{{\cos }^2}\alpha }}\;\end{array}$

$d) 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})$ $d) 1 + {\cot ^2}\alpha = \frac{1}{{{{\sin }^2}\alpha }}\;({0^o} < \alpha < {180^o})$

Ta có:

$\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}$ $\begin{array}{l}\cot \alpha = \frac{{\cos \alpha }}{{\sin \alpha }};\;\\ \Rightarrow \;1 + {\cot ^2}\alpha = 1 + \frac{{{{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{{{{\sin }^2}\alpha + {{\cos }^2}\alpha }}{{{{\sin }^2}\alpha }} = \frac{1}{{{{\sin }^2}\alpha }}\;\end{array}$

Bài 6 trang 65 Toán 10 Chân trời sáng tạo

Cho góc $\alpha$ $\alpha$ với $\cos \alpha = - \frac{{\sqrt 2 }}{2}$ $\cos \alpha = - \frac{{\sqrt 2 }}{2}$. Tính giá trị của biểu thức $A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .$ $A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha .$

Gợi ý đáp án

Ta có: $A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha$ $A = 2{\sin ^2}\alpha + 5{\cos ^2}\alpha = 2({\sin ^2}\alpha + {\cos ^2}\alpha ) + 3{\cos ^2}\alpha$

Mà ${\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.$ ${\cos ^2}\alpha + {\sin ^2}\alpha = 1;\cos \alpha = - \frac{{\sqrt 2 }}{2}.$

$\Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.$ $\Rightarrow A = 2 + 3.{\left( { - \frac{{\sqrt 2 }}{2}} \right)^2} = 2 + 3.\frac{1}{2} = \frac{7}{2}.$

Bài 7 trang 65 Toán 10 Chân trời sáng tạo

Dùng máy tính cầm tay, hãy thực hiện các yên cầu dưới đây:

a) Tính $\sin {168^o}45$ $\sin {168^o}45'33'';\cos {17^o}22'35'';\tan {156^o}26'39'';\cot {56^o}36'42''.$

b) Tìm $\alpha \;({0^o} \le \alpha \le {180^o})$ $\alpha \;({0^o} \le \alpha \le {180^o})$,trong các trường hợp sau:

$i) \sin \alpha = 0,862.$ $i) \sin \alpha = 0,862.$

$ii) \cos \alpha = - 0,567.$ $ii) \cos \alpha = - 0,567.$

$iii) \tan \alpha = 0,334.$ $iii) \tan \alpha = 0,334.$

Gợi ý đáp án

$\begin{array}{l}\sin {168^o}45$ $\begin{array}{l}\sin {168^o}45'33'' = 0,195;\\\cos {17^o}22'35'' = 0,954;\\\tan {156^o}26'39'' = - 0,436;\\\cot {56^o}36'42'' = 0,659\end{array}$

$i) \alpha = {59^o}32$ $i) \alpha = {59^o}32'30,8''.$

$ii) \alpha = {124^o}32$ $ii) \alpha = {124^o}32'28,65''.$

$iii) \alpha = {18^o}28$ $iii) \alpha = {18^o}28'9,55''.$

Chia sẻ bởi:

Trịnh Thị Thanh

Tải về

Bài trước

Bài sau

Liên kết tải về

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 315,3 KB

Tải về

Tìm thêm: Chân trời sáng tạo Chân trời sáng tạo Lớp 10

Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!

Sắp xếp theo

Tài liệu tham khảo khác

Chủ đề liên quan

Có thể bạn quan tâm

Xem thêm

Mới nhất trong tuần

Xem thêm

Tìm bài trong mục này

Đóng

Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm

Mua Download Pro 79.000đ

Tài khoản

Gói thành viên

Giới thiệu

Điều khoản

Bảo mật

Liên hệ

Facebook

Twitter

DMCA

Giấy phép số 569/GP-BTTTT. Bộ Thông tin và Truyền thông cấp ngày 30/08/2021. Cơ quan chủ quản: CÔNG TY CỔ PHẦN MẠNG TRỰC TUYẾN META. Địa chỉ: 56 Duy Tân, Phường Cầu Giấy, Hà Nội. Điện thoại: 024 2242 6188. Email: [email protected]. Bản quyền © 2025 download.vn.

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 Giải SGK Toán 10 trang 65 - Tập 1 sách Chân trời sáng tạo

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 0

Phần Thực hành Toán 10 Chân trời sáng tạo Bài 1

Thực hành 1

Thực hành 2

Bài tập Toán 10 trang 65 Chân trời sáng tạo

Bài 1 trang 65 Toán 10 Chân trời sáng tạo

Bài 2 trang 65 Toán 10 Chân trời sáng tạo

Bài 3 trang 65 Toán 10 Chân trời sáng tạo

Bài 4 trang 65 Toán 10 Chân trời sáng tạo

Bài 5 trang 65 Toán 10 Chân trời sáng tạo

Bài 6 trang 65 Toán 10 Chân trời sáng tạo

Bài 7 trang 65 Toán 10 Chân trời sáng tạo

Tải về

Tài liệu tham khảo khác

Toán 10 Bài tập cuối chương III - Chân trời sáng tạo

Toán 10 Bài 2: Hàm số bậc hai

Toán 10 Bài tập cuối chương II - Chân trời sáng tạo

Chủ đề liên quan

Có thể bạn quan tâm

Điều lệ Trường Mầm non - Ban hành kèm theo Thông tư số 52/2020/TT-BGDĐT

Kể lại truyền thuyết Sơn Tinh, Thủy Tinh bằng lời văn của em (2 Dàn ý + 21 mẫu)

Bài thu hoạch những nội dung chính trong công tác xây dựng Đảng ở cơ sở hiện nay

Ma trận đề thi học kì 2 lớp 5 năm 2024 - 2025 theo Thông tư 27

Tả cơn mưa rào mùa hạ - 3 Dàn ý & 35 bài văn tả cơn mưa lớp 5

Mẫu sáng kiến kinh nghiệm chuẩn - Mẫu sáng kiến kinh nghiệm dành cho giáo viên

Bộ đề thi học kì 2 môn Khoa học tự nhiên 8 năm 2024 - 2025 sách Cánh diều

Bộ đề thi học kì 2 môn Ngữ văn 8 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống

Đáp án cuộc thi Giao lưu tìm hiểu An toàn giao thông cho giáo viên năm 2022 - 2023

Văn mẫu lớp 12: Nghị luận xã hội về sự thành công trong cuộc sống

Mới nhất trong tuần

Toán 10 Bài tập cuối chương X - Chân trời sáng tạo

Toán 10 Bài 2: Đường thẳng trong mặt phẳng tọa độ

Toán 10 Bài 1: Dấu của tam thức bậc hai

Toán 10 Bài 1: Tọa độ của vectơ

Toán 10 Bài 2: Hệ bất phương trình bậc nhất hai ẩn

Toán 10 Bài 2: Định lí Côsin và định lí Sin

Toán 10 Bài 1: Bất phương trình bậc nhất hai ẩn

Toán 10 Bài 3: Các phép toán trên tập hợp

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180

Toán 10 Bài 2: Tập hợp

Toán 10 Bài 1: Giá trị lượng giác của một góc từ 0 đến 180 ⁰