Toán 10 Bài 18: Phương trình quy về phương trình bậc hai Giải SGK Toán 10 trang 27 - Tập 2 sách Kết nối tri thức với cuộc sống

Giải Toán lớp 10 trang 27 tập 2 Kết nối tri thức với cuộc sống giúp các bạn học sinh có thêm nhiều gợi ý tham khảo để trả lời các câu hỏi bài tập trong SGK bài 18 Phương trình quy về phương trình bậc hai thuộc chương 6 Hàm số, đồ thị và ứng dụng.

Toán 10 Kết nối tri thức trang 27 được biên soạn với các lời giải chi tiết, đầy đủ và chính xác bám sát chương trình sách giáo khoa môn Toán lớp 10. Giải Toán lớp 10 trang 27 Kết nối tri thức sẽ là tài liệu cực kì hữu ích hỗ trợ các em học sinh trong quá trình giải bài tập. Đồng thời phụ huynh có thể sử dụng để hướng dẫn con em học tập và đổi mới phương pháp giải phù hợp hơn. Vậy sau đây là trọn bộ bài giải Toán 10 bài 18: Phương trình quy về phương trình bậc hai mời các bạn cùng theo dõi.

Trả lời Hoạt động Toán 10 Bài 18

Hoạt động 1

Cho phương trình \(\sqrt{x^{2}-3x+2}=\sqrt{-x^{2}-2x+2}\)

a. Bình phương hai vế phương trình để khử căn và giải phương trình bậc hai nhận được.

b. Thử lại các giá trị tìm được ở câu a có thỏa mãn phương trình đã cho hay không.

Gợi ý đáp án

a. \(x^{2}-3x+2 = -x^{2}-2x+2\)

\(\Leftrightarrow\) \(2x^{2}-x=0\)

\(\Leftrightarrow x=\frac{1}{2}\) hoặc \(x=0\).

b. Các giá trị thỏa mãn phương trình đã cho.

Hoạt động 2

Cho phương trình \(\sqrt{26x^{2}-63x+38}= 5x-6\)

a. Bình phương hai vế và giải phương trình nhận được.

b. Thử lại các giá trị x tìm được ở câu a có thỏa mãn phương trình đã cho hay không.

Hướng dẫn giải:

a. \(26x^{2}-63x+38 = 25x^{2}-60x+36\)

\(\Leftrightarrow\) \(x^{2}-3x+2=0\)

\(\Leftrightarrow x=2\) hoặc x= 1.

b. Thử lại ta có:

• x = 1 không thỏa mãn phương trình đã cho.
• x =2 thỏa mãn phương trình đã cho.

Giải Toán 10 trang 27 Kết nối tri thức - Tập 2

Bài 6.20 trang 27

Giải các phương trình sau:

Gợi ý đáp án

\(a. \sqrt{3x^{2}-4x-1}=\sqrt{2x^{2}-4x+3}\)

Bình phương hai vế của phương trình ta được:

\(\Leftrightarrow x^{2}-4=0\)

\(\Leftrightarrow x = 2\) hoặc x = -2

Thử lại giá trị của x: đều thỏa mãn phương trình.

Vậy phương trình có nghiệm là x = 2 hoặc x = -2

\(b. \sqrt{x^{2}+2x-3}=\sqrt{-2x^{2}+5}\)

Bình phương hai vế của phương trình ta được:

\(x^{2}+2x-3=-2x^{2}+5\)

\(\Leftrightarrow 3x^{2}+2x-8=0\)

\(\Leftrightarrow x = -2\) hoặc \(x= \frac{4}{3}\)

Thử lại giá trị của x:

x = -2 không thỏa mãn phương trình,

\(x= \frac{4}{3}\) thỏa mãn phương trình.

Vậy nghiệm của phương trình là \(x= \frac{4}{3}.\)

\(c. \sqrt{2x^{2}+3x-3}=\sqrt{-x^{2}-x+1}\)

Bình phương hai vế của phương trình ta được:

\(2x^{2}+3x-3 = -x^{2}-x+1\)

\(\Leftrightarrow 3x^{2}+4x-4=0\)

\(\Leftrightarrow x = -2 hoặc x= \frac{2}{3}\)

Thử lại giá trị của x:

x = -2 không thỏa mãn phương trình,

\(x= \frac{2}{3}\) không thỏa mãn phương trình.

Vậy phương trình vô nghiệm.

\(d. \sqrt{-x^{2}+5x-4}=\sqrt{-2x^{2}+4x+3}\)

Bình phương hai vế của phương trình ta được:

\(-x^{2}+5x-4 = -2x^{2}+4x+3\)

\(\Leftrightarrow x^{2}+x-6=0\)

\(\Leftrightarrow x = 2\) hoặc x= -3

Thử lại giá trị của x:

x = 2 thỏa mãn phương trình,

x = -3 không thỏa mãn phương trình.

Vậy phương trình có nghiệm x = 2

Bài 6.21 trang 27

Giải các phương trình sau:

Gợi ý đáp án

\(a. \sqrt{6x^{2}+13x+13}=2x+4\)

Bình phương hai vế của phương trình ta được:

\(6x^{2}+13x+13 = 4x^{2}+16x+16\)

\(\Leftrightarrow 2x^{2}-3x-3 = 0\)

\(\Leftrightarrow x=\frac{3+\sqrt{33}}{4} hoặc x=\frac{3-\sqrt{33}}{4}\)

Thử lại giá trị đều thỏa mãn.

Vậy phương trình có nghiệm \(x=\frac{3+\sqrt{33}}{4} hoặc x=\frac{3-\sqrt{33}}{4}\)

\(b. \sqrt{2x^{2}+5x+3}=-3-x\)

Bình phương hai vế của phương trình ta được:

\(2x^{2}+5x+3 = 9+6x+x^{2}\)

\(\Leftrightarrow x^{2}-x-6 = 0\)

\(\Leftrightarrow x=3\) hoặc x=-2

Thử lại giá trị đều không thỏa mãn.

Vậy phương trình vô nghiệm.

\(c. \sqrt{3x^{2}-17x+23}=x-3\)

Bình phương hai vế của phương trình ta được:

\(3x^{2}-17x+23 = x^{2}-6x+9\)

\(\Leftrightarrow 2x^{2}-11x+14 = 0\)

\(\Leftrightarrow x=2\) hoặc \(x=\frac{7}{2}\)

Thử lại các giá trị:

• x = 2 không thỏa mãn
• \(x=\frac{7}{2}\) thõa mãn.

Vậy phương trình có nghiệm \(x=\frac{7}{2}\)

\(d. \sqrt{-x^{2}+2x+4}=x-2\)

Bình phương hai vế của phương trình ta được:

\(-x^{2}+2x+4 = x^{2}-4x+4\)

\(\Leftrightarrow -2x^{2}+6x= 0\)

\(\Leftrightarrow x=0\) hoặc x=3

Thử lại giá trị:

• x = 0 không thỏa mãn
• x = 3 thỏa mãn

Vậy phương trình có nghiệm là x = 3.

Bài 6.22 trang 27

Cho tứ giác ABCD có AB \bot CD; AB = 2; BC = 13; CD = 8; DA = 5. Gọi H là giao điểm của AB và CD và đặt x = AH. Hãy thiết lập một phương trình để tính độ dài x, từ đó tính diện tích tứ giác ABCD.

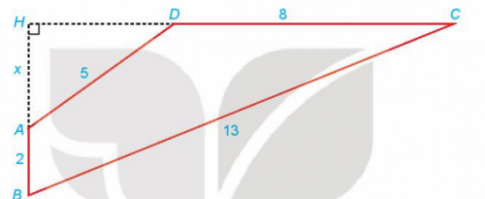
Gợi ý đáp án

• Xét tam giác AHD vuông tại H có: \(HD = \sqrt{25-x^{2}}\) (áp dụng định lí Pytago).
• Xét tam giác BHC vuông tại H có: \(HB^{2}+HC^{2}=BC^{2}\)

\(=> (x+2)^{2}+\left ( \sqrt{25-x^{2}} +8\right )^{2}=13^{2}\)

\(\Leftrightarrow 4\sqrt{25-x^{2}}=19-x\)

Bình phương hai vế ta được:

\(16.(25-x^{2}) =361 - 38x +x^{2}\)

\(\Leftrightarrow 17x^{2}-38x-39=0\)

\(\Leftrightarrow x= 3\) hoặc \(x= \frac{-13}{17}\)

Thử lại phương trình và điều kiện x > 0, giá trị x= 3 thỏa mãn.

Vậy AH = x = 3.

• Diện tích tam giác HAD là: \(S_{HAD}=\frac{1}{2}AH.HD=6\)
• Diện tích tam giác HBC là: \(S_{HAD}=\frac{1}{2}HB.HC=36\)

Vậy diện tích tứ giác ABCD là: 36 - 6 = 30 (đơn vị diện tích).

Bài 6.23 trang 27

Hằng ngày bạn Hùng đều đón bạn Minh đi học tại một vị trí trên lề đường thẳng đến trường. Minh đứng tại vị trí A cách lề đường một khoảng 50 m để chờ Hùng. Khi nhìn thấy Hùng đạp xe đến địa điểm B, cách mình một đoạn 200 m thì Minh bắt đầu đi bộ ra lề đường để bắt kịp xe. Vận tốc đi bộ Minh là 5 km/h, vận tốc xe đạp của Hùng là 15 km/h. Hãy xác định vị trí C trên lề đường để hai bạn gặp nhau mà không bạn nào phải chờ người kia (làm tròn kết quả đến hàng phần mười).

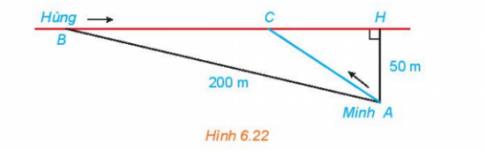
Gợi ý đáp án

Đặt CH = x (x >0)

Ta có: \(AC=\sqrt{x^{2}+50^{2}}=\sqrt{x^{2}+2500}\)

\(BH = \sqrt{200^{2}-50^{2}}=50\sqrt{15}\)

\(BC = BH - CH = 50\sqrt{15}-x\)

Vì hai bạn gặp nhau tại C, nên thời gian đi từ A đến C bằng thời gian đi từ B đến C, nên ta có phương trình:

\(\frac{50\sqrt{15}-x}{15}=\frac{\sqrt{x^{2}+2500}}{5}\)

\(\Leftrightarrow 50\sqrt{15}-x=3.\sqrt{x^{2}+2500}\)

Bình phương hai vế được:

\(37500-100\sqrt{15}.x+x^{2}=9.(x^{2}+2500)\)

\(\Leftrightarrow x\approx 25,4\) hoặc \(x\approx -73,8\)

Thử lại phương trình và điều kiện x >0 thì x = 25,4 thỏa mãn.

Vậy vị trí điểm C là cách H 1 khoảng 25,4 m.

Lý thuyết Phương trình quy về phương trình bậc hai

a. Phương trình chứa ẩn ở mẫu thức

Để giải phương trình chứa ẩn ở mẫu thức, ta có các bước giải như sau:

Bước 1. Tìm điều kiện xác định của ẩn của phương trình.

Bước 2. Quy đồng mẫu thức hai vế rồi khử mẫu.

Bước 3. Giải phương trình vừa nhận được ở bước 2.

Bước 4. So sánh các nghiệm tìm được ở bước 3 với điều kiện xác định và kết luận.

b. Phương trình đưa về dạng phương trình tích

Để giải phương trình đưa về dạng tích, ta có các bước giải như sau:

Bước 1. Phân tích vế trái thành nhân tử, vế phải bằng 0.

Bước 2. Xét từng nhân tử bằng 0 để tìm nghiệm.