Bài tập Nhân chia các số hữu tỉ Toán lớp 7 Nhân chia số hữu tỉ
Nhân chia số hữu tỉ thuộc dạng bài tập trọng tâm trong chương trình Toán 7. Chuyên đề Nhân chia số hữu tỉ bao gồm lý thuyết, các dạng toán và bài tập chuyên đề nhân, chia số hữu tỉ có đáp án kèm theo.
Toán lớp 7 Nhân chia số hữu tỉ được áp dụng với cả 3 bộ sách theo chương trình mới. Qua tài liệu này giúp các bạn học sinh nắm vững quy tắc nhân, chia hai số hữu tỉ, các tính chất của phép nhân số hữu tỉ. Từ đó vận dụng quy tắc nhân, chia số hữu tỉ để thực hiện phép tính, tính giá trị biểu thức. Vậy sau đây là Bài tập Nhân chia số hữu tỉ, mời các bạn cùng theo dõi tại đây.
Nhân chia số hữu tỉ
I. Lý thuyết Nhân chia các số hữu tỉ
1. Nhân hai số hữu tỉ
+ Phép nhân số hữu tỉ có các tính chất của phép nhân phân số: giao hoán, kết hợp, nhân với số 1
+ Với ![]() \(x = \frac{a}{b}\) và
\(x = \frac{a}{b}\) và ![]() \(y = \frac{c}{d}\left( {a,b,c,d \in Z} \right)\) ta có:
\(y = \frac{c}{d}\left( {a,b,c,d \in Z} \right)\) ta có: ![]() \(x.y = \frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}\)
\(x.y = \frac{a}{b}.\frac{c}{d} = \frac{{a.c}}{{b.d}}\)
2. Chia hai số hữu tỉ
+ Với ![]() \(x = \frac{a}{b}\) và
\(x = \frac{a}{b}\) và ![]() \(y = \frac{c}{d}\) ta có:
\(y = \frac{c}{d}\) ta có: ![]() \(x:y = \frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}}\)
\(x:y = \frac{a}{b}:\frac{c}{d} = \frac{a}{b}.\frac{d}{c} = \frac{{a.d}}{{b.c}}\)
+ Thương của phép chia số hữu tỉ x cho số hữu tỉ y (y khác 0) gọi là tỉ số của hai số x và y, kí hiệu là ![]() \(\frac{x}{y}\) hay x : y
\(\frac{x}{y}\) hay x : y
II. Sơ đồ hóa Nhân chia số hữu tỉ
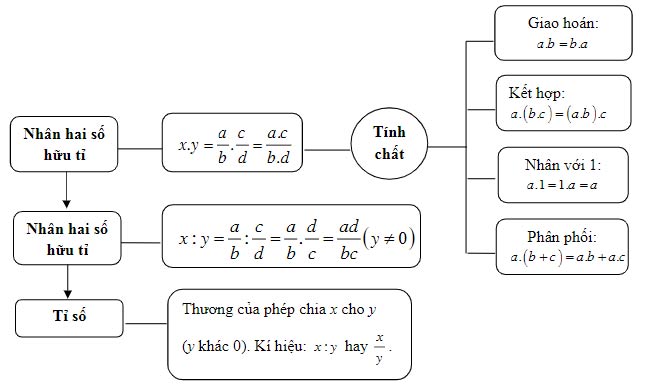
III. Ví dụ Nhân chia số hữu tỉ
Ví dụ 1:
a) ![]() \(\dfrac{-2}{7}.\dfrac{21}{8}\)
\(\dfrac{-2}{7}.\dfrac{21}{8}\)
b) ![]() \(0,24.\dfrac{-15}{4}\)
\(0,24.\dfrac{-15}{4}\)
c) ![]() \((-2).\left(-\dfrac{7}{12}\right)\)
\((-2).\left(-\dfrac{7}{12}\right)\)
d) ![]() \(\left(-\dfrac{3}{25}\right) : 6\)
\(\left(-\dfrac{3}{25}\right) : 6\)
a) ![]() \(\dfrac{-2}{7}.\dfrac{21}{8}\)
\(\dfrac{-2}{7}.\dfrac{21}{8}\) ![]() \(= \dfrac{-2.21}{7.8} = \dfrac{-3}{4};\)
\(= \dfrac{-2.21}{7.8} = \dfrac{-3}{4};\)
b) ![]() \(0,24.\dfrac{-15}{4}\)
\(0,24.\dfrac{-15}{4}\) ![]() \(\dfrac{6}{25}.\dfrac{-15}{4} = \dfrac{6.(-15)}{25.4} = \dfrac{-9}{10};\)
\(\dfrac{6}{25}.\dfrac{-15}{4} = \dfrac{6.(-15)}{25.4} = \dfrac{-9}{10};\)
c) ![]() \((-2).\left(-\dfrac{7}{12}\right) = \dfrac{-2}{1}.\left(-\dfrac{7}{12}\right) = \dfrac{(-2).(-7)}{1.12} = \dfrac{7}{6};\)
\((-2).\left(-\dfrac{7}{12}\right) = \dfrac{-2}{1}.\left(-\dfrac{7}{12}\right) = \dfrac{(-2).(-7)}{1.12} = \dfrac{7}{6};\)
d) ![]() \(\left(-\dfrac{3}{25}\right) : 6 = \left(-\dfrac{3}{25}\right). \dfrac{1}{6}= \dfrac{(-3).1}{25.6} = \dfrac{-1}{50}\)
\(\left(-\dfrac{3}{25}\right) : 6 = \left(-\dfrac{3}{25}\right). \dfrac{1}{6}= \dfrac{(-3).1}{25.6} = \dfrac{-1}{50}\)
Ví dụ 2:
Ta có thể viết số hữu tỉ ![]() \(\dfrac{-5}{16}\) dưới các dạng sau đây:
\(\dfrac{-5}{16}\) dưới các dạng sau đây:
a) ![]() \(\dfrac{-5}{16}\) là tích của hai số hữu tỉ. Ví dụ:
\(\dfrac{-5}{16}\) là tích của hai số hữu tỉ. Ví dụ: ![]() \(\dfrac{-5}{16} = \dfrac{-5}{2}.\dfrac{1}{8};\)
\(\dfrac{-5}{16} = \dfrac{-5}{2}.\dfrac{1}{8};\)
b) ![]() \(\dfrac{-5}{16}\) là thương của hai số hữu tỉ. Ví dụ:
\(\dfrac{-5}{16}\) là thương của hai số hữu tỉ. Ví dụ:![]() \(\dfrac{-5}{16} = \dfrac{-5}{2} : 8\)
\(\dfrac{-5}{16} = \dfrac{-5}{2} : 8\)
Với mỗi câu, em hãy tìm thêm một ví dụ.
Theo đề bài ta có:
a) ![]() \(\dfrac{-5}{16} = \dfrac{-5}{4}.\dfrac{1}{4} = (-5).\dfrac{1}{16} = \dfrac{-5}{8}.\dfrac{1}{2};\)
\(\dfrac{-5}{16} = \dfrac{-5}{4}.\dfrac{1}{4} = (-5).\dfrac{1}{16} = \dfrac{-5}{8}.\dfrac{1}{2};\)
b)![]() \(\dfrac{-5}{16} = \dfrac{-5}{4} : 4 = \dfrac{-5}{8} : 2\)
\(\dfrac{-5}{16} = \dfrac{-5}{4} : 4 = \dfrac{-5}{8} : 2\)
Lưu ý:![]() \(\dfrac{a}{b}. \dfrac{c}{d} = \dfrac{a.c}{b.d}\)
\(\dfrac{a}{b}. \dfrac{c}{d} = \dfrac{a.c}{b.d}\)
Ví dụ 3
Tính:
a) ![]() \(\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right);\)
\(\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right);\)
b) ![]() \((-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right);\)
\((-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right);\)
c) ![]() \(\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5};\)
\(\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5};\)
d) ![]() \(\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]\)
\(\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]\)
a) ![]() \(\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right)\)
\(\dfrac{-3}{4}.\dfrac{12}{-5}.\left(-\dfrac{25}{6}\right)\)
![]() \(= \dfrac{-3.(-12).(-25)}{4.5.6}\)
\(= \dfrac{-3.(-12).(-25)}{4.5.6}\)
![]() \(= \dfrac{-15}{2} = -7\dfrac{1}{2}\)
\(= \dfrac{-15}{2} = -7\dfrac{1}{2}\)
b) ![]() \((-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right)\)
\((-2).\dfrac{-38}{21}.\dfrac{-7}{4}.\left(-\dfrac{3}{8}\right)\)
![]() \(= \dfrac{(-2).(-38).(-7).(-3)}{21.4.8}\)
\(= \dfrac{(-2).(-38).(-7).(-3)}{21.4.8}\)
![]() \(= \dfrac{19}{8} = 2\dfrac{3}{8}\)
\(= \dfrac{19}{8} = 2\dfrac{3}{8}\)
c) ![]() \(\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5}\)
\(\left(\dfrac{11}{12}:\dfrac{33}{16}\right).\dfrac{3}{5}\)
![]() \(= \left(\dfrac{11}{12}.\dfrac{16}{33}\right).\dfrac{3}{5}\)
\(= \left(\dfrac{11}{12}.\dfrac{16}{33}\right).\dfrac{3}{5}\)
![]() \(= \dfrac{11.16.3}{12.33.5}\)
\(= \dfrac{11.16.3}{12.33.5}\)
![]() \(= \dfrac{4}{15}\)
\(= \dfrac{4}{15}\)
d) ![]() \(\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]\)
\(\dfrac{7}{23}.\left[\left(-\dfrac{8}{6}\right)-\dfrac{45}{18}\right]\)
![]() \(= \dfrac{7}{23}.\dfrac{-24 - 25}{18}\)
\(= \dfrac{7}{23}.\dfrac{-24 - 25}{18}\)
![]() \(= \dfrac{7}{23}.\left(\dfrac{-69}{18}\right)\)
\(= \dfrac{7}{23}.\left(\dfrac{-69}{18}\right)\)
![]() \(= \dfrac{7.(-69)}{23.18}\)
\(= \dfrac{7.(-69)}{23.18}\)
![]() \(= -\dfrac{7}{6}\)
\(= -\dfrac{7}{6}\)
![]() \(= -1\dfrac{1}{6}\)
\(= -1\dfrac{1}{6}\)
Ví dụ 4:
a) -0,32 . (-0,875)
![]() \(= \frac{{ - 32}}{{100}}.\left( {\frac{{ - 875}}{{1000}}} \right)\)
\(= \frac{{ - 32}}{{100}}.\left( {\frac{{ - 875}}{{1000}}} \right)\)
![]() \(= \frac{{ - 8}}{{25}}.\left( {\frac{{ - 7}}{8}} \right) = \frac{{ - 7}}{{25}}\)
\(= \frac{{ - 8}}{{25}}.\left( {\frac{{ - 7}}{8}} \right) = \frac{{ - 7}}{{25}}\)
b) ![]() \(\left( { - 5} \right):2\frac{1}{5} = \left( { - 5} \right):\frac{{11}}{5} = \left( { - 5} \right).\frac{5}{{11}} = \frac{{ - 25}}{{11}}\)
\(\left( { - 5} \right):2\frac{1}{5} = \left( { - 5} \right):\frac{{11}}{5} = \left( { - 5} \right).\frac{5}{{11}} = \frac{{ - 25}}{{11}}\)
Ví dụ 5:
Ngăn đựng sách của một giá sách trong thư viện dài 120cm (xem hình bên). Người ta dự định xếp các cuốn sách dày khoảng 2,4 cm vào ngăn này. Hỏi ngăn sách đó có thể để được nhiều nhất bao nhiêu cuốn sách như vậy?
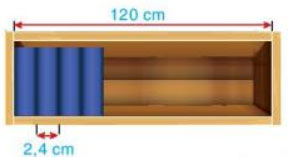
Gợi ý đáp án:
Ngăn sách đó có thể để được số sách nhiều nhất là:
120 : 2, 4 = 50 (cuốn sách)
Vậy có thể để được nhiều nhất 50 cuốn sách vào ngăn sách đó.
Ví dụ 6;
b) ![]() \(\left( {7 - \frac{1}{2} - \frac{3}{4}} \right):\left( {5 - \frac{1}{4} - \frac{5}{8}} \right)\)
\(\left( {7 - \frac{1}{2} - \frac{3}{4}} \right):\left( {5 - \frac{1}{4} - \frac{5}{8}} \right)\)
![]() \(= \left( {\frac{{28}}{4} - \frac{2}{4} - \frac{3}{4}} \right):\left( {\frac{{40}}{8} - \frac{2}{8} - \frac{5}{8}} \right)\)
\(= \left( {\frac{{28}}{4} - \frac{2}{4} - \frac{3}{4}} \right):\left( {\frac{{40}}{8} - \frac{2}{8} - \frac{5}{8}} \right)\)
![]() \(= \left( {\frac{{28 - 2 - 3}}{4}} \right):\left( {\frac{{40 - 2 - 5}}{8}} \right)\)
\(= \left( {\frac{{28 - 2 - 3}}{4}} \right):\left( {\frac{{40 - 2 - 5}}{8}} \right)\)
![]() \(= \frac{{23}}{4}:\frac{{33}}{8} = \frac{{23}}{4}.\frac{8}{{33}} = \frac{{46}}{{33}}\)
\(= \frac{{23}}{4}:\frac{{33}}{8} = \frac{{23}}{4}.\frac{8}{{33}} = \frac{{46}}{{33}}\)
IV. Bài tập Nhân chia các số hữu tỉ
Câu 1: Kết quả của phép tính ![]() \(\frac{{ - 3}}{4}.\frac{{16}}{{15}}\) bằng:
\(\frac{{ - 3}}{4}.\frac{{16}}{{15}}\) bằng:
| A. |
B. |
C. -1 | D. |
Câu 2: Kết quả của phép tính ![]() \(\frac{{22}}{4}:\frac{{11}}{8}\) bằng:
\(\frac{{22}}{4}:\frac{{11}}{8}\) bằng:
| A. 1 | B. 2 | C. 3 | D. 4 |
Câu 3: Giá trị x thỏa mãn ![]() \(\frac{3}{4}x = \frac{{15}}{{16}}\) là:
\(\frac{3}{4}x = \frac{{15}}{{16}}\) là:
| A. |
B. |
C. |
D. |
Câu 4: ![]() \(\frac{{ - 1}}{6}\) là kết quả của phép tính:
\(\frac{{ - 1}}{6}\) là kết quả của phép tính:
| A. |
B. |
| C. |
D. |
Câu 5: Giá trị x thỏa mãn ![]() \(x:\frac{5}{4} = \frac{8}{{15}}\) là:
\(x:\frac{5}{4} = \frac{8}{{15}}\) là:
| A. |
B. |
C. |
D. |
Câu 6: Thực hiện phép tính:
| a, |
b, |
c, |
| d, |
e, |
f, |
Câu 7: Tìm số hữu tỉ x, biết:
| a, |
b, |
| c, |
d, |
Câu 8: Viết số hữu tỉ ![]() \(\frac{{ - 25}}{{16}}\) dưới các dạng:
\(\frac{{ - 25}}{{16}}\) dưới các dạng:
a, Tích của hai số hữu tỉ có một thừa số là ![]() \(\frac{{ - 5}}{{12}}\)
\(\frac{{ - 5}}{{12}}\)
b, Thương của hai số hữu tỉ, trong đó số bị chia là ![]() \(\frac{{ - 4}}{5}\)
\(\frac{{ - 4}}{5}\)
V. Đáp án bài tập Nhân chia các số hữu tỉ
| Câu 1 | Câu 2 | Câu 3 | Câu 4 | Câu 5 |
| B | D | D | C | A |
Câu 6
| a, |
b, |
c, |
| d, |
e, |
f, |
Câu 7:
| a, |
b, |
c, |
d, |
Câu 8
a, ![]() \(\frac{{ - 25}}{{16}} = \frac{{ - 5}}{{12}}.\frac{{15}}{4}\)
\(\frac{{ - 25}}{{16}} = \frac{{ - 5}}{{12}}.\frac{{15}}{4}\)
b, ![]() \(\frac{{ - 25}}{{16}} = \frac{{ - 4}}{5}:\frac{{64}}{{125}}\)
\(\frac{{ - 25}}{{16}} = \frac{{ - 4}}{5}:\frac{{64}}{{125}}\)
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Tả cơn mưa rào mùa hạ - 3 Dàn ý & 35 bài văn tả cơn mưa lớp 5
-

Mẫu sáng kiến kinh nghiệm chuẩn - Mẫu sáng kiến kinh nghiệm dành cho giáo viên
-

Bộ đề thi học kì 2 môn Khoa học tự nhiên 8 năm 2024 - 2025 sách Cánh diều
-

Bộ đề thi học kì 2 môn Ngữ văn 8 năm 2024 - 2025 sách Kết nối tri thức với cuộc sống
-

Đáp án cuộc thi Giao lưu tìm hiểu An toàn giao thông cho giáo viên năm 2022 - 2023
-

Văn mẫu lớp 12: Nghị luận xã hội về sự thành công trong cuộc sống
-

Văn mẫu lớp 12: Nghị luận xã hội cách nuôi dưỡng vẻ đẹp tâm hồn
-

Soạn bài Tự đánh giá: Gói thuốc lá Cánh diều
-

Đề cương ôn tập học kì 2 môn Lịch sử - Địa lí lớp 5 năm 2024 - 2025 (Sách mới)
-

Bộ đề thi học kì 2 môn Hoạt động trải nghiệm hướng nghiệp 7 sách Kết nối tri thức với cuộc sống
Mới nhất trong tuần
-

Toán 7 Luyện tập chung trang 44
5.000+ -

Toán 7 Bài 34: Sự đồng quy của ba trung tuyến, ba đường phân giác trong một tam giác
1.000+ -

Toán 7 Bài tập cuối chương VI - Kết nối tri thức với cuộc sống
5.000+ -

Toán 7 Bài 23: Đại lượng tỉ lệ nghịch
1.000+ -

Toán 7 Luyện tập chung trang 70
5.000+ -

Toán 7 Luyện tập chung trang 19
1.000+ -

Toán 7 Bài 22: Đại lượng tỉ lệ thuận
1.000+ -

Toán 7 Bài 21: Tính chất của dãy tỉ số bằng nhau
1.000+ -

Bài tập Tết môn Toán lớp 7 năm 2024 - 2025
10.000+ -

Toán 7 Luyện tập chung trang 10
10.000+






 Toán 7 Kết nối tri thức
Toán 7 Kết nối tri thức
 Toán 7 Chân trời sáng tạo
Toán 7 Chân trời sáng tạo
 Toán 7 Cánh Diều
Toán 7 Cánh Diều
 Soạn Văn 7 Chân trời sáng tạo
Soạn Văn 7 Chân trời sáng tạo
 Soạn Văn 7 Cánh Diều
Soạn Văn 7 Cánh Diều
 Soạn Văn 7 Kết nối tri thức
Soạn Văn 7 Kết nối tri thức
 Tiếng Anh 7 Global Success
Tiếng Anh 7 Global Success
 Tiếng Anh 7 Explore English
Tiếng Anh 7 Explore English
 Tiếng Anh 7 - iLearn Smart World
Tiếng Anh 7 - iLearn Smart World