30 đề thi tuyển sinh vào lớp 10 chuyên môn Toán
TỔNG HỢP 30 ĐỀ THI TUYỂN SINH VÀO LỚP 10 CHUYÊN
MÔN: TOÁN
ĐỀ THI TUYỂN SINH LỚP 10 HỆ THPT CHUYÊN ĐHKHTN, ĐHQG HÀ NỘI
NĂM HỌC: 2007 - 2008.
Thời gian: 150 phút
Câu 1. (3 điểm)
Giải hệ phương trình và phương trình sau:
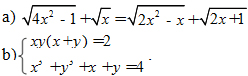
Câu 2. (3 điểm)
a) Giả sử x1, x2 là 2 nghiệm dương của phương trình x2 – 4x + 1 = 0. Chứng minh rằng x1 + x2 là một số nguyên.
b) Cho a, b là các số nguyên dương thỏa mãn a + 1 và b + 2007 đều chia hết cho 6. Chứng minh rằng 4a + a + b chia hết cho 6.
Câu 3. (3 điểm)
Cho M là trung điểm của cung nhỏ AB của đường tròn tâm O (AB không phải là đường kính). C và D là 2 điểm phân biệt, thay đổi nằm giữa A và B. Các đường thẳng MC, MD cắt (O) tương ứng tại E, F khác M.
a) Chứng minh các điểm C, D, E, F nằm trên một đường tròn.
b) Gọi O1 và O2 lần lượt là tâm các đường tròn ngoại tiếp các tam giác ACE và BDF. Chứng minh rằng khi C và D thay đổi trên đoạn AB thì giao điểm của hai đường thẳng AO1 và BO2 là một điểm cố định.
Câu 4. (1 điểm)
Cho a, b, c là các số thực dương thỏa mản abc = 1. Chứng minh rằng:![]()
ĐẠI HỌC QUỐC GIA TP HỒ CHÍ MINH
ĐỀ THI TUYỂN SINH LỚP 10 NĂNG KHIẾU NĂM HỌC 2007 - 2008
MÔN TOÁN AB (Chung cho các lớp Toán, Tin, Lý, Hoá, Sinh)
Thời gian làm bài: 150 phút.
Câu 1. Cho phương trình:![]()
a) Tìm m để x = -1 là một nghiệm của phương trình (1)
b) Tìm m để phương trình (1) vô nghiệm
Câu 2.
a) Giải bất phương trình: |(x +3)( x - 1)| - 2|x - 1| < x2 - 7
b) Giải hệ phương trình: 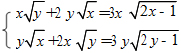
Câu 3.
a) Cho a, b là hai số thoả mãn điều kiện: a2 - 3ab + b2 + a - b = a2 - 2ab + b2 - 5a + 7b = 0
Chứng tỏ rằng: ab - 12a + 15b = 0
b) Cho: ![]()
Hãy tìm tất cả các giá trị của x để A3 < 0
Câu 4. Cho tam giác ABC nhọn có H là trực tâm và góc BAC bằng 60o. Gọi M, N, P lần lượt là chân đường cao kẻ từ A, B, C của tam giác ABC là I là trung điểm của BC.
a) Chứng minh rằng tam giác INP đều
b) Gọi E và K lần lượt là trung điểm của PB và NC. Chứng minh các điểm I, M, E và K cùng thuộc một đường tròn
c) Giả sử IA là phân giác của góc NIP. Hãy tính số đo của góc BCP
Câu 5.
Một công ty may giao cho tổ A may 16800 sản phẩm, tổ B may 16500 sản phẩm và bắt đầu thực hiện công việc cùng một lúc. Nếu sau 6 ngày, tổ A được hỗ trợ thêm 10 công nhân may thì họ hoàn thành công việc cùng lúc với tổ B. Nếu tổ A được hỗ trợ thêm 10 công nhân may ngay từ đầu thì họ sẽ hoàn thành công việc sớm hơn tổ B 1 ngày. Hãy xác định số công nhân ban đầu của mỗi tổ. Biết rằng, mỗi công nhân may mỗi ngày được 20 sản phẩm.
Download tài liệu để xem chi tiết.
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Đoạn văn nghị luận về tính kỷ luật (Dàn ý + 20 Mẫu)
-

Đoạn văn nghị luận về biến đổi khí hậu (Dàn ý + 14 mẫu)
-

Phiếu báo thay đổi hộ khẩu, nhân khẩu
-

Viết bài văn kể lại một chuyến đi đáng nhớ của em ngắn gọn (13 mẫu)
-

11 câu phân tích kế hoạch bài dạy cấp THCS
-

Nghị luận xã hội về kỹ năng sống (3 Dàn ý + 18 mẫu)
-

Bộ đề kiểm tra 1 tiết môn tiếng Anh lớp 7 thí điểm Chương trình mới
-

Viết bài văn nghị luận về một vấn đề đời sống (trình bày ý kiến phản đối)
-

Tổng hợp bài tập Toán lớp 2 cơ bản và nâng cao
-

Mở bài gián tiếp Tả cây ăn quả (11 mẫu)
Mới nhất trong tuần
-

Đề thi thử vào lớp 10 năm học 2018 – 2019 môn Ngữ Văn (Có đáp án)
100.000+ -

Điểm chuẩn lớp 10 năm 2025 Tuyên Quang
10.000+ 1 -

Điểm chuẩn lớp 10 năm 2025 TP Hồ Chí Minh
5.000+ -

Điểm chuẩn lớp 10 năm 2025 Khánh Hòa
50.000+ 1 -

Điểm chuẩn lớp 10 năm 2025 Hà Nội
50.000+ -

Điểm chuẩn lớp 10 năm 2025 Đồng Tháp
10.000+ -

Điểm chuẩn lớp 10 năm 2025 Quảng Trị
5.000+ -

Điểm chuẩn lớp 10 năm 2025 Cao Bằng
1.000+ -

Điểm chuẩn lớp 10 năm 2025 Hòa Bình
5.000+ -

Điểm chuẩn lớp 10 năm 2025 Sơn La
5.000+






 Lớp 2
Lớp 2
 Lớp 4
Lớp 4
 Lớp 5
Lớp 5
 Thi vào 6
Thi vào 6
 Lớp 6
Lớp 6
 Lớp 7
Lớp 7
 Lớp 9
Lớp 9