Eballsviet.com
Học tập Lớp 10 Lớp 12 Toán 12

Tư duy dồn biến trong bất đẳng thức Tài liệu ôn tập môn Toán lớp 10

Giới thiệu Tải về Bình luận

Nhằm đem đến cho các bạn học sinh có thêm nhiều tài liệu học tập môn Toán chuyên đề Bất đẳng thức, Eballsviet.com giới thiệu tài liệu Tư duy dồn biến trong bất đẳng thức.

Đây là tài liệu hữu ích, gồm 13 bài toán bất đẳng thức được xử lý bằng phương pháp dồn biến. Tài liệu có đáp án chi tiết kèm theo. Hy vọng với tài liệu này các bạn có thêm nhiều tài liệu tham khảo củng cố kiến thức đạt được kết quả cao trong các bài kiểm tra, bài thi THPT Quốc gia sắp tới.

Tư duy dồn biến trong bất đẳng thức

I. Giới thiệu cơ bản về bất đẳng thức Cauchy (AM – GM):
Bất đẳng thức Cauchy cho hai số:
a b ab a b
ab
ab a b
2
2 , , 0
,,
2




. Đẳng thức xảy ra khi
ab
.
Bất đẳng thức Cauchy cho ba số:
a b c a bc a b c
a b c
abc a b c
3
3
3 , , , 0
, , , 0
3




. Đẳng thức xảy ra khi
a b c
Bất đẳng thức Cauchy tổng quát cho
n
số không âm:
n
n n n
n
n
nn
a a a n a a a a a a
a a a
a a a a a a
n
1 2 1 2 1 2
12
1 2 1 2
... ... , , ,... 0
...
... , , ,... 0



. Đẳng thức xảy ra khi
n
a a ... a
12
II. Các hệ quả của bất đẳng thức Cauchy (AM – GM):
a b ab, a,b
22
2
. Đẳng thức xảy ra khi
.
a b ab, a,b
22
2
. Đẳng thức xảy ra khi
.
ab
ab
2
2



, a,b
. Đẳng thức xảy ra khi
.
a b c abc, a,b,c
3 3 3
30
. Đẳng thức xảy ra khi
a b c
.
a b c
abc
3
3




, a,b,c 0
. Đẳng thức xảy ra khi
a b c
.
ab bc ca a b c a b c a b c
2
2 2 2
3 3 , , ,
. Đẳng thức xảy ra khi
a b c
.
a b ab a b a b
33
, , 0
. Đẳng thức xảy ra khi
.
ab
a b a b
ba
22
, , 0
. Đẳng thức xảy ra khi
ab
.
IV. Sử dụng bất đẳng thức AM – GM đưa về biến cần tìm:
Bài 1: Cho các số thực
,xy
thỏa mãn
xy0
. Tìm giá trị nhỏ nhất của:
P x y x y
33
23
.
Bài 2: Cho các số thực
,xy
dương. Tìm giá trị nhỏ nhất của biểu thức:
P x y
xy x y
22
1
8
8
.
Bài 3: Cho các số thực dương
xy,
. Tìm giá trị nhỏ nhất của biểu thức:
P
xy
x y x y
3 3 3 3
11
9

24H HỌC TOÁN - CHIẾN THẮNG 3 CÂU PHÂN LOẠI
Giáo viên: Đoàn Trí Dũng – Hà Hữu Hải
BÀI 6: AM – GM Dồn biến
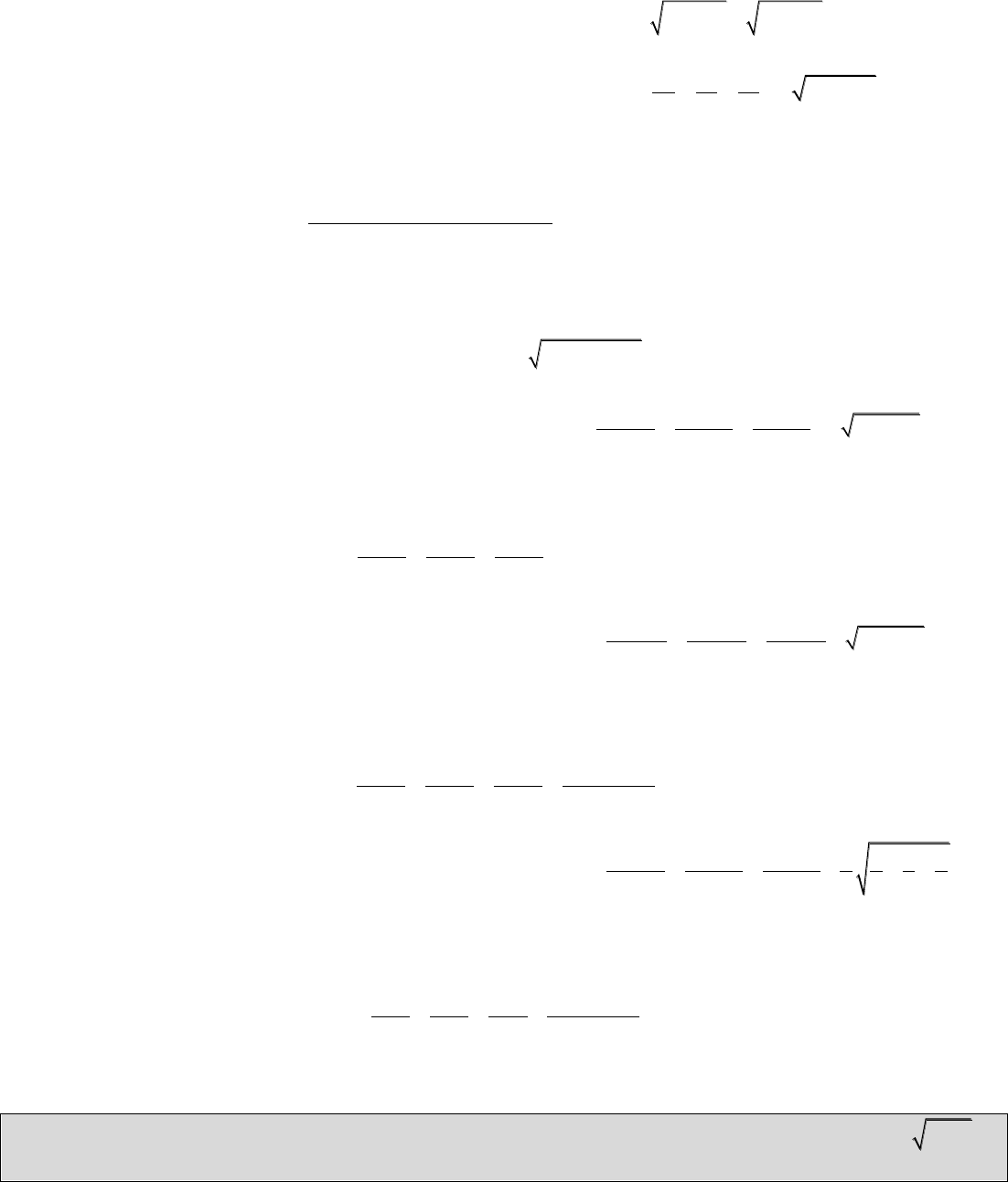
Bài 4: Cho
,,a b c
thỏa mãn
c a c b c0, ,
. Tìm giá trị lớn nhất của:
22
2 P c a c c b c a b
Bài 5: Cho các số thực
a b c, , 0
. Tìm giá trị nhỏ nhất của biểu thức:
2
ab bc ca
P a b c
c a b
Bài 6: Cho
a b c,,
độ dài 3 cạnh một tam giác. Tìm giá trị nhỏ nhất của biểu thức:
2 2 2
1
1
P a b c abc
a b c b c a c a b
.
Bài 7: Cho các số thực dương
xyz,,
thỏa mãn
xyz 1
. Tìm giá trị nhỏ nhất của biểu thức:
4 4 4
3
3 P x y y z z x xy yz zx
Bài 8: Cho các số thực
a b c,,
dương. Tìm giá trị nhỏ nhất của:
2 2 2
4
4
a bc b ca c ab
P a b c
b c c a a b
Bài 9: Cho các số thực dương
a b c,,
thỏa mãn
3 a b c
. Tìm giá trị nhỏ nhất của biểu thức:
3
2 2 2
1 1 1
a b c
P a b c
b c a
.
Bài 10: Cho các số thực dương
a b c,,
. Tìm giá trị nhỏ nhất của:
3 3 3
2 2 2 2 2 2
abc
P a b c
a b b c c a
Bài 11: Cho các số thực dương
a b c,,
thỏa mãn điều kiện
1abc
. Tìm giá trị nhỏ nhất của biểu thức:
3
2 2 2
1 1 1
54
1 1 1

a b c
a b c
P
b c a
Bài 12: Cho các số thực dương
a b c,,
. Tìm giá trị nhỏ nhất của:
3 3 3
3 3 3 3
2
a b c
P
a b c
b ab c bc a ca
Bài 13: Cho các số thực dương
a b c,,
thỏa mãn
abc 1
. Tìm giá trị lớn nhất của biểu thức:
2
1 1 1
1 1 1 6

a b c
a b c
P
b c a
ĐÁP ÁN
Bài 1: Cho các số thực
,xy
thỏa mãn
xy0
. Tìm giá trị nhỏ nhất của biểu thức:
P x y x y
33
23
.
Phân tích
Biến cần đưa về:
xy
.
Chiều đánh giá cần có:
P
.
Chiều cần đánh giá cần tìm:
x y f x y
33
.
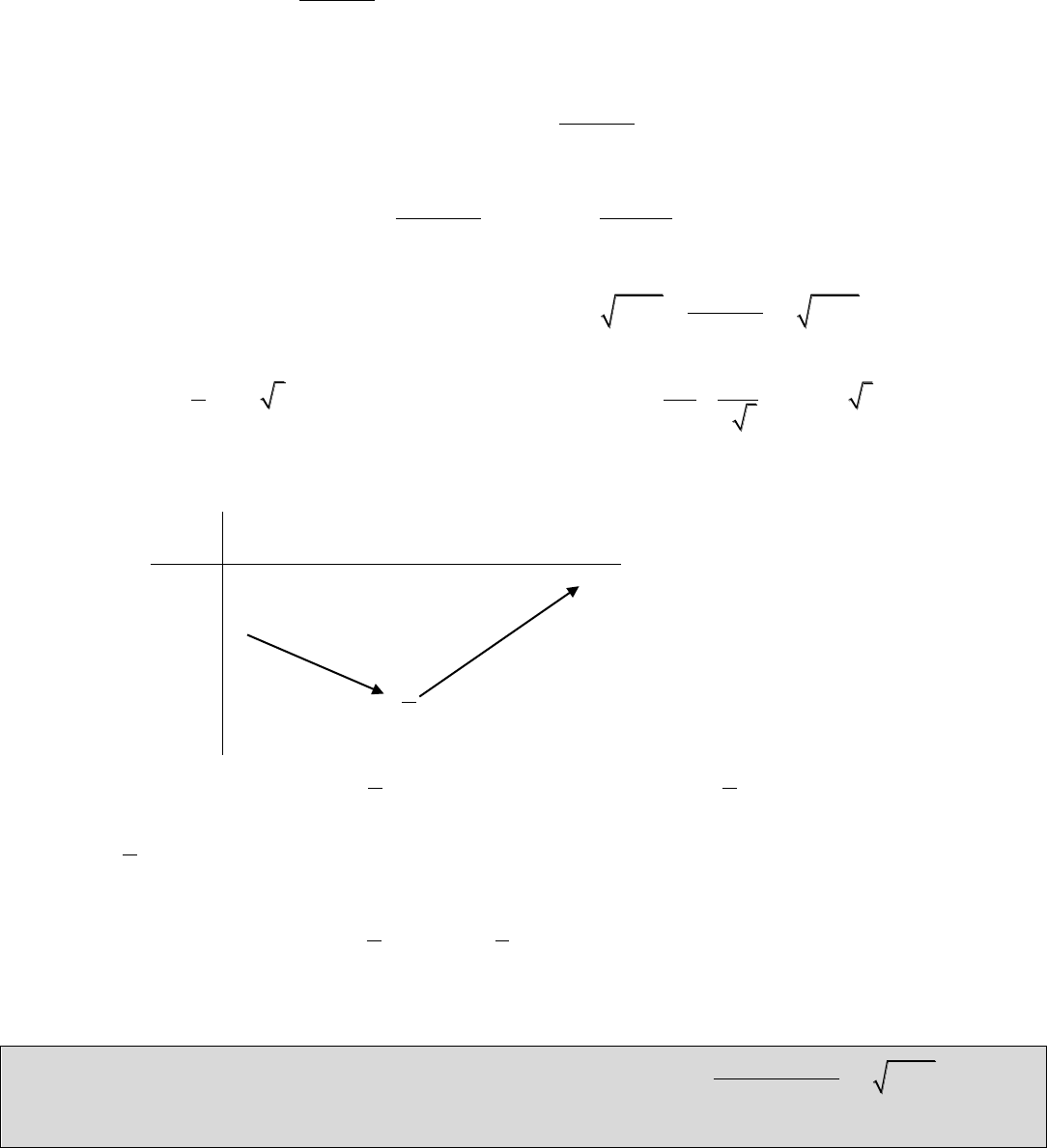
Biến đổi biểu thức:
x y x y xy x y
3
33
3
, do đó nếu muốn sử dụng đánh giá
x y x y
33
, ta sẽ cần
xy x y
.
Đánh giá cần tìm:
xy
xy
2
4
.
Bài giải
Ta có:
x y x y xy x y
3
33
3
. Ta có đánh giá:
xy
xy
2
4
. Do đó:
x y x y
x y x y xy x y x y x y
33
33
3 3 3 3
3
3
44

Đẳng thức xảy ra khi và chỉ khi:
xy
. Vậy:
xy
P x y x y x y
3
33
2 3 3
2
.
Xét hàm số
f t t t t
3
1
3 , 0
2
. Ta có:
P f x y
. Vì:
t
f t t t t
t
2
2
33
' 0 1 1
2
2
.
Do đó ta có bảng biến thiên:
t
0 1

ft

0
5
2
Từ bảng biến thiên, ta thấy
ft
5
2

t, 0; 
. Vậy
P f x y
5
2
. Đẳng thức xảy ra khi và chỉ
khi
xy
1
2

.
Kết luận: Giá trị nhỏ nhất của
P
là
5
2
tại
xy
1
2

.
Bài 2: Cho các số thực
,xy
dương. Tìm giá trị nhỏ nhất của biểu thức:
P x y
xy x y
22
1
8
8
.
Phân tích
Biến cần đưa về:
xy
.
Chiều đánh giá cần có:
P
.
Chiều cần đánh giá cần tìm:
xy x y f x y
22
.
Liên kết tải về
Tìm thêm: Toán 10 Toán 12

Tài liệu tham khảo khác

Có thể bạn quan tâm

Xem thêm
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ

Mới nhất trong tuần