Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số Giải Toán 12 Cánh diều trang 21 → 27

Giải Toán 12 Bài 3: Đường tiệm cận của đồ thị hàm số là tài liệu vô cùng hữu ích giúp các em học sinh có thêm nhiều gợi ý tham khảo để giải các bài tập trong SGK Toán 12 Cánh diều tập 1 trang 21, 22, 23, 24, 25, 26, 27.

Giải bài tập Toán 12 Cánh diều tập 1 Bài 3 được trình bày rõ ràng, cẩn thận, dễ hiểu nhằm giúp học sinh nhanh chóng biết cách làm bài. Đồng thời, cũng là tài liệu hữu ích giúp giáo viên thuận tiện trong việc hướng dẫn học sinh ôn tập Bài 3 Chương I: Ứng dụng đạo hàm để khảo sát và vẽ đồ thị của hàm số. Mời thầy cô và các em theo dõi bài viết dưới đây của Eballsviet.com:

Giải Toán 12 Cánh diều Tập 1 trang 27

Bài 1

Tiệm cận đứng của đồ thị hàm số \(y = \frac{x+2}{x+1}\) là:

Đáp án đúng: A

Bài 2

Tiệm cận xiên của đồ thị hàm số \(y = \frac{x^{2} +3x+5}{x+2}\) là:

Đáp án đúng: B

Bài 3

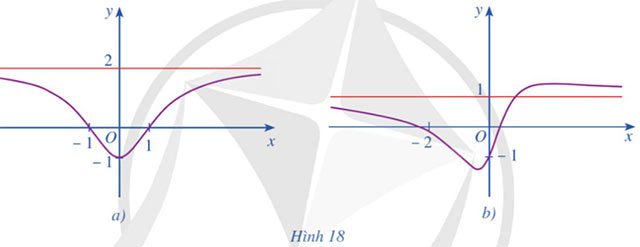
Đồ thị hàm số ở Hình 18a, Hình 18b đều có đường tiệm cận ngang là đường thẳng màu đỏ. Hỏi đó là đồ thị của hàm số nào trong các hàm số sau?

a) \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\)

b) \(y = \frac{{2{x^2} + x + 1}}{{x - 1}}\)

c) \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\)

Hướng dẫn giải:

a) Ta có: \(\lim_{x \rightarrow + \infty} f(x) = \lim_{x \rightarrow + \infty} \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}} =1 ;\)

\(\ \lim_{x \rightarrow - \infty} f(x) = \lim_{x \rightarrow - \infty} \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}} =1\)

b) Ta có: \(\lim_{x \rightarrow + \infty} f(x) = \lim_{x \rightarrow + \infty} \frac{{2{x^2} + x + 1}}{{x - 1}} =+\infty ;\)

\(\lim_{x \rightarrow - \infty} f(x) = \lim_{x \rightarrow - \infty} \frac{{2{x^2} + x + 1}}{{x - 1}} =-\infty\)

c) Ta có: \(\lim_{x \rightarrow + \infty} f(x) = \lim_{x \rightarrow + \infty} \frac{{2{x^2} - 2}}{{{x^2} + 2}} = 2 ;\)

\(\lim_{x \rightarrow - \infty} f(x) = \lim_{x \rightarrow - \infty} \frac{{2{x^2} - 2}}{{{x^2} + 2}} = 2\)

Vậy hình 18a là đồ thị của hàm số \(y = \frac{{2{x^2} - 2}}{{{x^2} + 2}}\)

hình 18b là đồ thị của hàm số \(y = \frac{{{x^2} + 2x - 1}}{{{x^2} + 1}}\)

Bài 4

Tìm tiệm cận đứng, tiệm cận ngang, tiệm cận xiên (nếu có) của đồ thị mỗi hàm số sau:

a) \(y = \frac{x}{{2 - x}}\)

b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}}\)

c) \(y = x - 3 + \frac{1}{{{x^2}}}\)

Hướng dẫn giải:

a) \(y = \frac{x}{{2 - x}}\)

Ta có: \(\lim_{x\rightarrow +\infty} \frac{x}{{2 - x}} =-1; \lim_{x\rightarrow -\infty} \frac{x}{{2 - x}} =-1\)

Vậy y = - 1 là tiệm cận ngang của đồ thị hàm số đã cho.

\(\lim_{x\rightarrow 2^+ } \frac{x}{{2 - x}} =-\infty ; \lim_{x\rightarrow 2^-} \frac{x}{{2 - x}} =+ \infty\)

Vậy x = 2 là tiệm cận đứng của đồ thị hàm số đã cho.

b) \(y = \frac{{2{x^2} - 3x + 2}}{{x - 1}} = 2x-1+\frac{1}{{x - 1}}\)

c) \(y = x - 3 + \frac{1}{{{x^2}}}\)

Bài 5

Số lượng sản phẩm bán được cho một công ty trong x (tháng) được tính theo công thức

\(S\left( x \right) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\) trong đó \(x \ge 1\)

a) Xem y = S(x) là một hàm số xác định trên nửa khoảng \([1; + \infty )\), hãy tìm tiệm cận ngang của đồ thị hàm số đó.

b) Nêu nhận xét về số lượng sản phẩm bán được của công ty đó trong x (tháng) khi x đủ lớn.

Hướng dẫn giải:

a) Xét hàm số \(y=S\left( x \right) = 200\left( {5 - \frac{9}{{2 + x}}} \right)\)

Ta có \(\lim_{x \rightarrow +\infty} S(x) = \lim_{x \rightarrow +\infty}200\left( {5 - \frac{9}{{2 + x}}} \right) =1000\)

\(\lim_{x \rightarrow -\infty} S(x) = \lim_{x \rightarrow -\infty}200\left( {5 - \frac{9}{{2 + x}}} \right) =1000\)

Vậy y = 1 000 là tiệm cận ngang của đồ thị hàm số y = S(x).

b) Khi x càng lớn thì số lượng sản phẩm bán được của công ty đó trong x (tháng) sẽ tiến gần đến 1 000 sản phẩm.