Các dạng toán nguyên hàm trong đề thi THPT Quốc gia Các dạng toán nguyên hàm trong đề thi THPT Quốc gia
Eballsviet.com xin giới thiệu đến quý thầy cô cùng các bạn học sinh lớp 12 tài liệu Các dạng toán nguyên hàm trong đề thi THPT Quốc gia.
Đây là tài liệu vô cùng hữu ích, gồm 75 trang tuyển tập các câu hỏi và bài toán trắc nghiệm chủ đề nguyên hàm cùng các vấn đề liên quan, có đáp án và lời giải chi tiết, các câu hỏi và bài toán được tác giả trích dẫn từ các đề thi THPT Quốc gia môn Toán những năm gần đây. Mời các bạn cùng tham khảo và tải tài liệu tại đây.
Các dạng toán nguyên hàm trong đề thi THPT Quốc gia
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Ngu
yễn Bảo Vương: https://www.facebook.com/phong.baovuong 1
CHUYÊN
ĐỀ 18
NGUYÊN HÀM & PHƯƠNG PHÁP TÌM NGUYÊN HÀM
MỤC LỤC
PHẦN
A. CÂU HỎI ......................................................................................................................................................... 2
Dạng 1. Nguyên hàm cơ bản (dùng bảng nguyên hàm) ................................................................................................... 2
Dạng 1.1 Tìm nguyên hàm cơ bản không có điều kiện ................................................................................................ 2
Dạng 1.2 Tìm nguyên hàm cơ bản có điều kiện ......................................................................................................... 11
Dạng 2. Sử dụng phương pháp VI PHÂN để tìm nguyên hàm ...................................................................................... 16
Dạng 2.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 16
Dạng 2.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 17
Dạng 3. Sử dụng phương pháp ĐỔI BIẾN để tìm nguyên hàm ..................................................................................... 18
Dạng 3.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 18
Dạng 3.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 21
Dạng 4. Nguyên hàm từng phần ..................................................................................................................................... 22
Dạng 4.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 22
Dạng 4.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 25
Dạng 5. Sử dụng nguyên hàm để giải toán ..................................................................................................................... 26
Dạng 6. Một số bài toán khác liên quan đến nguyên hàm .............................................................................................. 30
PHẦN B. ĐÁP ÁN THAM KHẢO ............................................................................................................................... 33
Dạng 1. Nguyên hàm cơ bản (dùng bảng nguyên hàm) ................................................................................................. 33
Dạng 1.1 Tìm nguyên hàm cơ bản không có điều kiện .............................................................................................. 33
Dạng 1.2 Tìm nguyên hàm cơ bản có điều kiện ......................................................................................................... 38
Dạng 2. Sử dụng phương pháp VI PHÂN để tìm nguyên hàm ...................................................................................... 44
Dạng 2.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 44
Dạng 2.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 45
Dạng 3. Sử dụng phương pháp ĐỔI BIẾN để tìm nguyên hàm ..................................................................................... 47
Dạng 3.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 47
Dạng 3.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 51
Dạng 4. Nguyên hàm từng phần ..................................................................................................................................... 53
Dạng 4.1 Tìm nguyên hàm không có điều kiện .......................................................................................................... 53
Dạng 4.2 Tìm nguyên hàm có điều kiện..................................................................................................................... 57
Dạng 5. Sử dụng nguyên hàm để giải toán ..................................................................................................................... 60
Dạng 6. Một số bài toán khác liên quan đến nguyên hàm .............................................................................................. 69
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 2
PHẦN A. CÂU HỎI
Dạng 1. Nguyên hàm cơ bản (dùng bảng nguyên hàm)
Dạng 1.1 Tìm nguyên hàm cơ bản không có điều kiện
Câu 1. (MĐ 103 BGD&ĐT NĂM 2017-2018) Nguyên hàm của hàm số
4 2
f x x x
là
A.
5 3
1 1
5 3
x x C
B.
4 2
x x C
C.
5 3
x x C
. D.
3
4 2
x x C
Câu 2. (Mã đề 104 - BGD - 2019) Họ tất cả nguyên hàm của hàm số
2 4
f x x
là
A.
2
x C
. B.
2
2
x C
. C.
2
2 4
x x C
. D.
2
4
x x C
.
Câu 3. (Mã 102 - BGD - 2019) Họ tất cả các nguyên hàm của hàm số
2 6
f x x
là
A.
2
x C
. B.
2
6
x x C
. C.
2
2
x C
. D.
2
2 6
x x C
.
Câu 4. (MĐ 105 BGD&ĐT NĂM 2017) Tìm nguyên hàm của hàm số
2 sinf x x
.
A.
2 sin 2 cos
xdx x C
B.
2 sin 2 cos
xdx x C
C.
2
2 sin sin
xdx x C
D.
2 sin sin 2
xdx x C
Câu 5. (Mã đề 101 BGD&ĐT NĂM 2018) Nguyên hàm của hàm số
3
f x x x
là
A.
4 2
1 1
4 2
x x C
B.
2
3 1
x C
C.
3
x x C
D.
4 2
x x C
Câu 6. (Mã 103 - BGD - 2019) Họ tất cả các nguyên hàm của hàm số
2 3f x x
là
A.
2
3
x x C
. B.
2
2 3
x x C
. C.
2
x C
. D.
2
2
x C
.
Câu 7. (ĐỀ MINH HỌA GBD&ĐT NĂM 2017) Tìm nguyên hàm của hàm số
2 1.
f x x
A.
2
2 1 2 1 .
3
f x dx x x C
B.
1
2 1 2 1 .
3
f x dx x x C
C.
1
2 1 .
3
f x dx x C
D.
1
2 1 .
2
f x dx x C
Câu 8. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2017) Tìm nguyên hàm của hàm số
2
2
2
f x x
x
.
A.
3
1
d
3
x
f x x C
x
. B.
3
2
d
3
x
f x x C
x
.
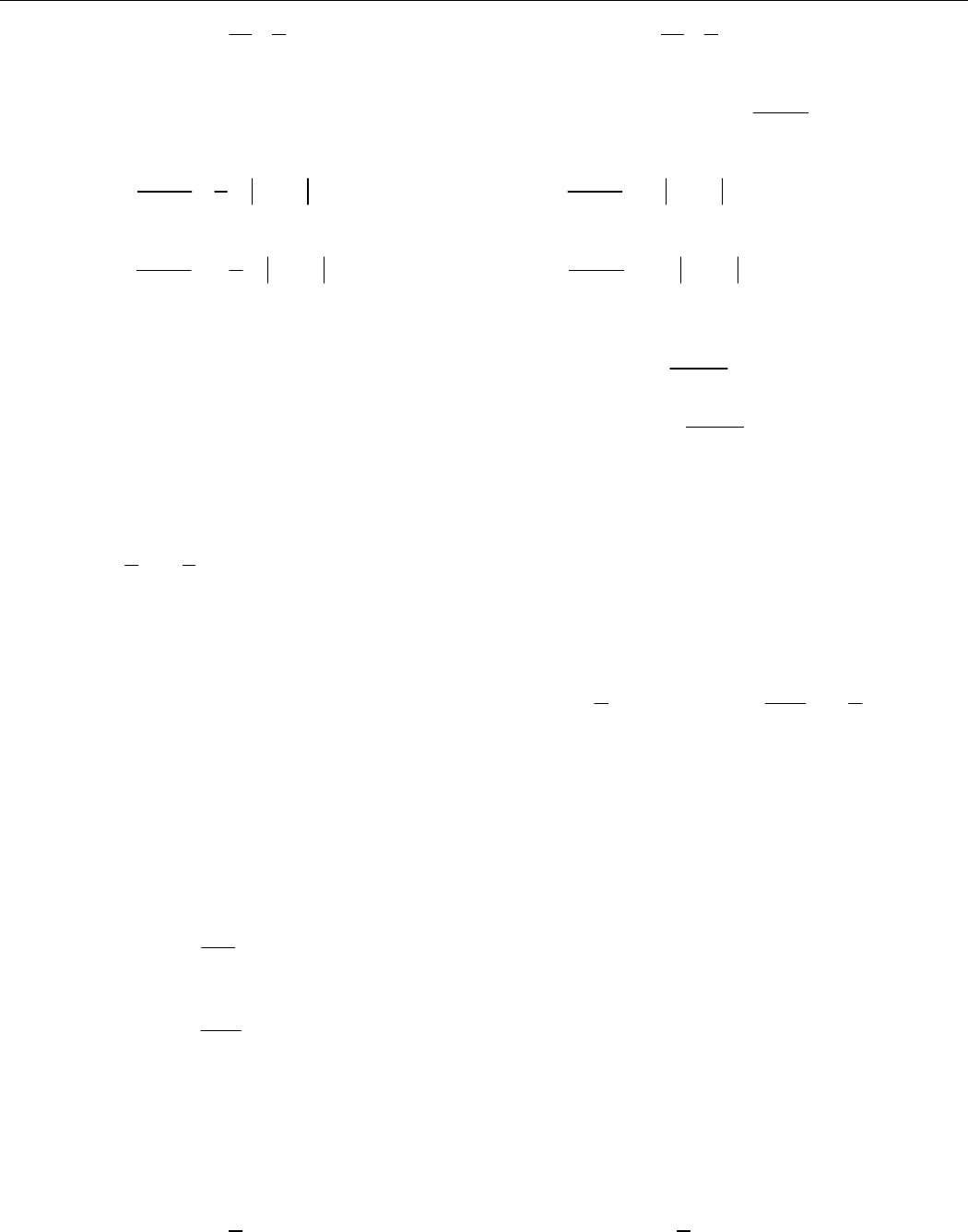
CÁC DẠNG TOÁN THƯỜNG GẶP TRONG KỲ THI THPTQG ĐT:0946798489
Nguyễn Bảo Vương: https://www.facebook.com/phong.baovuong 3
C.
3
1
d
3
x
f x x C
x
. D.
3
2
d
3
x
f x x C
x
.
Câu 9. (MÃ ĐỀ 110 BGD&ĐT NĂM 2017) Tìm nguyên hàm của hàm số
1
5 2
f x
x
.
A.
d 1
ln 5 2
5 2 5
x
x C
x
B.
d
ln 5 2
5 2
x
x C
x
C.
d 1
ln 5 2
5 2 2
x
x C
x
D.
d
5ln 5 2
5 2
x
x C
x
Câu 10. (MÃ ĐỀ 123 BGD&DT NĂM 2017) Tìm nguyên hàm của hàm số
cos 3f x x
A.
cos 3 3sin 3
xdx x C
B.
sin 3
cos 3
3
x
xdx C
C.
cos 3 sin 3
xdx x C
D.
sin 3
cos 3
3
x
xdx C
Câu 11. (Mã đề 104 BGD&ĐT NĂM 2018) Nguyên hàm của hàm số
3 2
f x x x
là
A.
4 3
1 1
4 3
x x C
B.
2
3 2
x x C
C.
3 2
x x C
D.
4 3
x x C
Câu 12. (ĐỀ THAM KHẢO BGD&ĐT NĂM 2018-2019) Họ nguyên hàm của hàm số
x
f x e x
là
A.
1
x
e C
B.
2x
e x C
C.
2
1
2
x
e x C
D.
2
1 1
1 2
x
e x C
x
Câu 13. (Mã đề 101 - BGD - 2019) Họ tất cả các nguyên hàm của hàm số
( ) 2 5f x x
là
A.
2
x C
. B.
2
5
x x C
. C.
2
2 5
x x C
. D.
2
2
x C
.
Câu 14. (MĐ 104 BGD&DT NĂM 2017) Tìm nguyên hàm của hàm số
7
x
f x
.
A.
7
7 d
ln 7
x
x
x C
B.
1
7 d 7
x x
x C
C.
1
7
7 d
1
x
x
x C
x
D.
7 d 7 ln 7
x x
x C
Câu 15. Tìm nguyên hàm của hàm số
cos2
f x x
.
A.
d 2sin 2
f x x x C
B.
d 2sin 2
f x x x C
C.
1
d sin 2
2
f x x x C
D.
1
d sin 2
2
f x x x C
Câu 16. (Mã đề 102 BGD&ĐT NĂM 2018) Nguyên hàm của hàm số
4
f x x x
là
Liên kết tải về
Các dạng toán nguyên hàm trong đề thi THPT Quốc gia
848,7 KB
Tải về
Có thể bạn quan tâm
-
Văn mẫu lớp 12: Dàn ý phân tích khổ 3 bài thơ Việt Bắc (6 Mẫu)
-
Toán 6 Bài 3: Làm tròn số thập phân và ước lượng kết quả
-
Đáp án Cuộc thi Tuyên truyền quy tắc ứng xử năm 2021
-
Văn mẫu lớp 9: Phân tích hai khổ cuối bài thơ Viếng lăng Bác
-
Hợp đồng đặt cọc mua bán nhà đất - Mẫu hợp đồng đặt cọc mua đất mới nhất
-
Hợp đồng mua bán hàng hóa - Hợp đồng mua bán mới nhất 2020
-
Bài dự thi Người anh hùng nhỏ tuổi chí lớn (8 mẫu)
-
Văn mẫu lớp 10: Phân tích bài thơ Tỏ lòng của Phạm Ngũ Lão
-
Văn mẫu lớp 9: Nghị luận xã hội Lá lành đùm lá rách
-
Ngữ pháp tiếng Anh cơ bản bằng sơ đồ tư duy
Xác thực tài khoản!
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Số điện thoại chưa đúng định dạng!
Sắp xếp theo
Đóng
Chỉ thành viên Download Pro tải được nội dung này!
Download Pro - Tải nhanh, website không quảng cáo!
Tìm hiểu thêm
Mới nhất trong tuần
-
Đề thi thử THPT Quốc gia năm 2025 môn Ngữ văn trường THPT Yên Dũng 2, Bắc Giang
100+ -
Các dạng bài tập cực trị của hàm số
50.000+ -
Tóm tắt lý thuyết và giải nhanh Toán 12
50.000+ 1 -
Các dạng bài tập tính đơn điệu của hàm số
50.000+ -
524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia
5.000+ -
Bộ đề thi chọn học sinh giỏi môn Toán lớp 12
10.000+ -
Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024
10.000+ -
Lý thuyết và bài tập trắc nghiệm số phức
100+ -
Hướng dẫn giải các dạng toán tiệm cận của đồ thị hàm số
1.000+ -
Bài tập trắc nghiệm ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
1.000+