Eballsviet.com
Học tập Lớp 12 Toán 12

Bài toán cực trị số phức Giải bài toán cực trị số phức bằng phương pháp hình học

Giới thiệu Tải về Bình luận

Bài toán cực trị số phức là một trong những bài toán khá thú vị trong chương trình Toán lớp 12 và cũng là một trong những dạng toán khó dành cho học sinh.

Hiểu rõ được điều đó, Eballsviet.com xin giới thiệu đến các bạn Bài toán cực trị số phức để các bạn dễ dàng hình dung và nắm bắt được kiến thức trọng tâm. Sau đây là nội dung chi tiết, mời bạn đọc cùng tham khảo và tải tài liệu tại đây.

Bài toán cực trị số phức

1
CỰC TRỊ SỐ PHỨC VÀ HÌNH HỌC
Câu 1. Cho số phức z thỏa mãn điều kiện |z − 1 − i| + |z + 1 + 3i| = 6
√
5. Giá trị lớn nhất của
|z −2 −3i| là
A 5
√
5. B 2
√
5. C 6
√
5. D 4
√
5.
Hướng dẫn giải
Ta có |z −1 − i| + |z + 1 + 3i| = 6
√
5 ⇔ MA + MB = 6
√
5 với M(x; y)
biểu diễn số phức z = x + yi, A(1; 1) biểu diễn số phức 1 + i, B(−1; −3)
biểu diễn số phức −1 −3i.
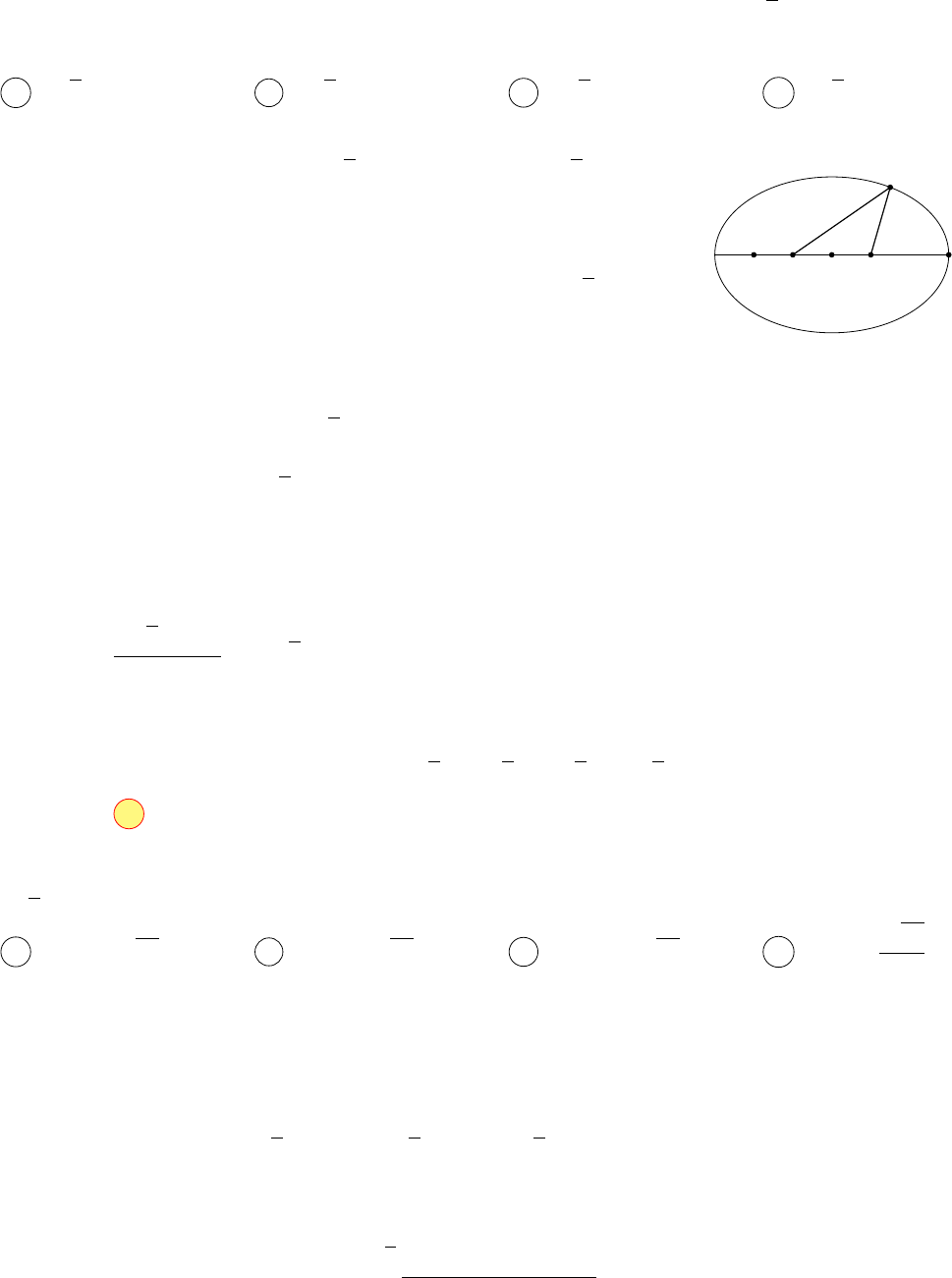
Khi đó điểm M nằm trên elip tâm I có độ dài trục lớn 6
√
5 và A, B là
hai tiêu điểm.
A
B
C
I
M
0
M
• |z −2 −3i| = MC với C(2; 3) biểu diễn số phức 2 + 3i.
•
# »
AB = (−2; −4) ⇒ AB = 2
√
5.
•
# »
A C = (1; 2) ⇒ AC =
√
5.
• Vì
# »
AB = −2
# »
A C nên
# »
AB,
# »
A C ngược hướng và AB = 2AC.
Gọi M
0
là điểm nằm trên elip sao cho A, B, M
0
thẳng hàng và M
0
khác phía A so với B.
Ta có BM
0
=
6
√
5 − AB
2
= 2
√
5.
Ta thấy MC ≤ M
0
C với mọi điểm M nằm trên elip.
Do đó MC lớn nhất khi và chỉ khi M ≡ M
0
.
Khi đó MC = M
0
C = CA + AB + BM
0
=
√
5 + 2
√
5 + 2
√
5 = 5
√
5.
Chọn đáp án A
Câu 2. Cho số phức z thỏa mãn |z + 1| + |z − 3 − 4i| = 10. Giá trị nhỏ nhất P
min
của biểu thức
P = |z − 1 + 2i| bằng
A P
min
=
√
17. B P
min
=
√
34. C P
min
= 2
√
10. D P
min
=
√
34
2
.
Hướng dẫn giải
Đặt z = x + yi, điểm biểu diễn của z là M(x; y).
Khi đó |z + 1| + |z −3 −4i| = 10 ⇔ MA + MB = 10 với A(−1; 0) và B(3; 4).
Suy ra M thuộc elip có độ dài trục lớn là 10 ⇒ 2a = 10 ⇒ a = 5 và hai tiêu điểm là A, B.
Mà
# »
AB = (4; 4) ⇒ AB = 4
√
2 ⇒ 2c = 4
√
2 ⇒ c = 2
√
2.
Ta có
P = |z −1 + 2i|
=
q
(x −1)
2
+ (y −2)
2
= MH
2
Với H(1; 2). Dễ thấy A, B, H thẳng hàng nên H thuộc đoạn AB.
Do đó P
min
⇔ MH ngắn nhất khi và chỉ khi M thuộc trục nhỏ của elip.
Khi đó độ dài MH bằng một nửa trục nhỏ hay MH = b =
√
a
2
−c
2
=
√
17.
Chọn đáp án A
Câu 3. Cho các số phức z, w thỏa mãn |z − 5 + 3i| = 3, |iw + 4 + 2i| = 2. Tìm giá trị lớn nhất của
biểu thức T = |3iz + 2w|.
A
√
554 + 5. B
√
578 + 13. C
√
578 + 5. D
√
554 + 13.
Hướng dẫn giải
O
IA B
9
4
Ta có |z −5 + 3i| = 3 ⇔
3iz −15i −9
3i
= 3 ⇔ |3iz −9 −15i| = 9.
|iw + 4 + 2i| = 2 ⇔
−i
2
(−2w −4 + 8i)
= 2 ⇔ |−2w −4 + 8i| = 4.
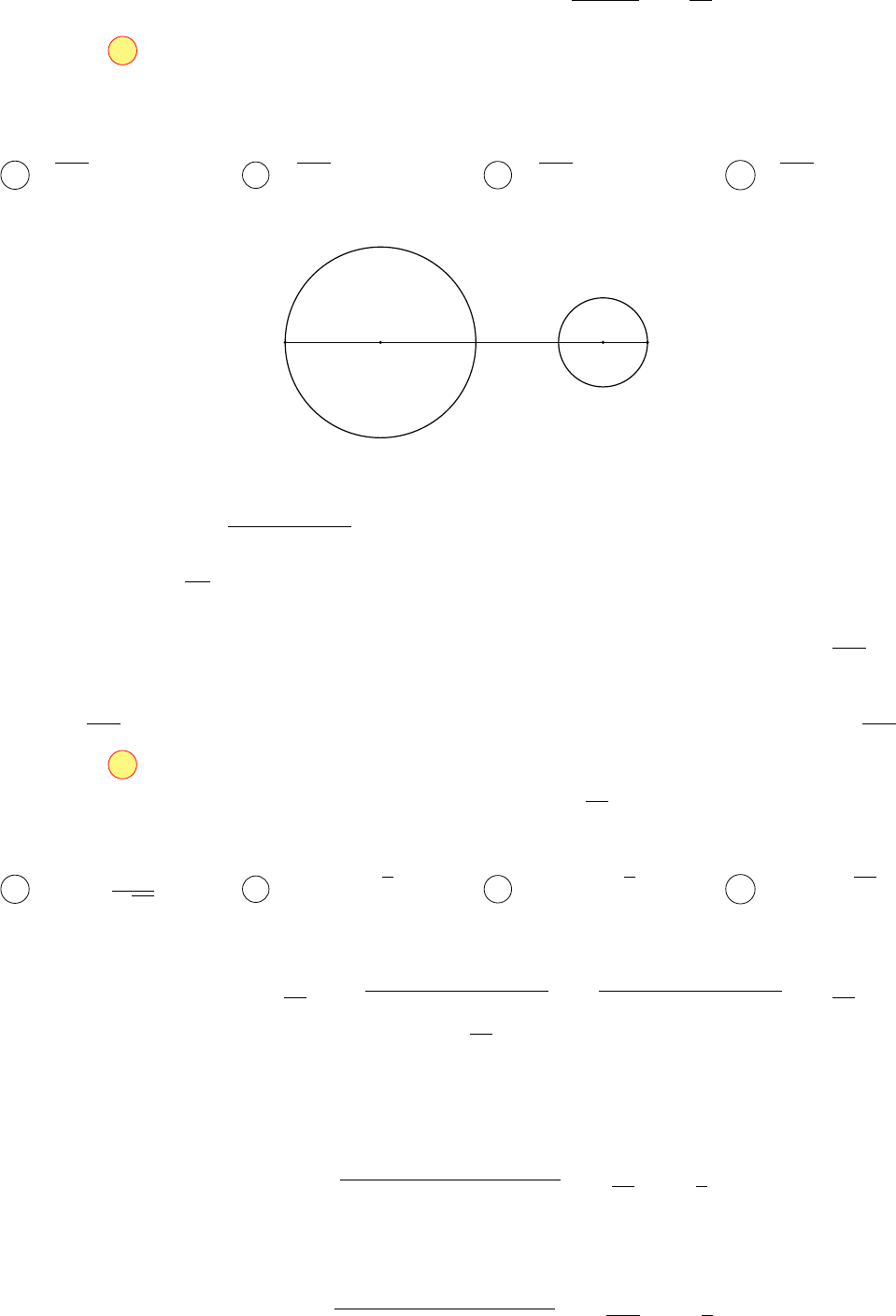
Gọi A và B là điểm biểu diễn của 3iz và −2w, khi đó A và B lần lượt thuộc các đường tròn tâm
O(9; 15) bán kính bằng 9 và đường tròn I(4; −8) bán kính bằng 4. Ta tính được OI =
√
554.
Khi đó T = |3iz + 2w| = |3iz − (−2w)| = AB.
Do IO =
√
554 > 4 + 9 nên hai đường tròn ngoài nhau, suy ra AB
max
= AO + OI + IB =
√
554 + 13.
Chọn đáp án D
Câu 4. Xét số phức z thỏa mãn
|
iz −2i −2
|
−
|
z + 1 −3i
|
=
√
34. Tìm giá trị nhỏ nhất của biểu thức
P =
|
(1 + i)z + 2i
|
.
A P
min
=
9
√
17
. B P
min
= 3
√
2. C P
min
= 4
√
2. D P
min
=
√
26.
Hướng dẫn giải
Giả sử số phức z có dạng z = a + bi, z có biểu diễn hình học là điểm M(a; b). Khi đó
|
iz −2i −2
|
−
|
z + 1 −3i
|
=
√
34 ⇔
q
(b + 2)
2
+ (a −2)
2
−
q
(a + 1)
2
+ (b −3)
2
=
√
34. (1)
Gọi điểm A(2; −2), B(−1; 3) khi đó ta có AB =
√
34. Kết hợp với (1) ta suy ra MA − MB = AB. ⇒
Điểm M trùng với điểm B hoặc B là trung điểm của MA. Ta xét hai trường hợp sau:
• TH1: M trùng B ⇒ M (−1; 3). Suy ra
P =
q
(a − b)
2
+ (a + b + 2)
2
=
√
32 = 4
√
2.
• TH2: B là trung điểm của MA ⇒ M(−4; 8). Suy ra
P =
q
(a − b)
2
+ (a + b + 2)
2
=
√
180 = 6
√
5.
3
Suy ra, min P = 4
√
2.
Chọn đáp án C
Câu 5. Cho số phức z thỏa mãn
z −2i
z + 3 −i
= 1. Giá trị nhỏ nhất của |z + 3 −2i| bằng
A
2
√
10
5
. B 2
√
10. C
√
10. D
√
10
5
.
Hướng dẫn giải
Gọi z = x + yi với x, y ∈ R.
z −2i
z + 3 −i
= 1 ⇔ |z −2i| = |z + 3 − i| ⇔
|
x + (y −2)i
|
=
|
(x + 3) + (y − 1)i
|
⇔ 3x + y + 3 = 0.
Vậy tập hợp các điểm biểu diễn số phức z là đường thẳng d : 3x + y + 3 = 0.
Ta có |z + 3 −2i| = |z − (−3 + 2i)|, với M
0
(−3; 2).
|z + 3 −2i| đạt giá trị nhỏ nhất bằng d(M
0
, d) =
|−9 + 2 + 3|
√
9 + 1
=
4
√
10
=
2
√
10
5
.
Chọn đáp án A
Câu 6. Cho các số phức z, w thỏa mãn |z| =
√
5, w = (4 − 3i)z + 1 − 2i. Giá trị nhỏ nhất của |w|
là
A 3
√
5. B 4
√
5. C 5
√
5. D 6
√
5.
Hướng dẫn giải
Theo giả thiết ta có w = (4 − 3i)z + 1 − 2i ⇒ z =
w −1 + 2i
4 −3i
.
Nên |z| =
√
5 ⇔
w −1 + 2i
4 −3i
=
√
5 ⇔
|
w −1 + 2i
|
= 5
√
5.
Vậy, tập hợp điểm biểu diễn số phức w là đường tròn I(1; −2) và bán kính R = 5
√
5.
Ta có OI =
p
1
2
+ (−2)
2
=
√
5 < R.
Do đó min |w| = R −OI = 5
√
5 −
√
5 = 4
√
5.
Chọn đáp án B
Câu 7. Cho số phức z thỏa mãn |z −3 + 4i| = 2. Mô-đun lớn nhất của z bằng
A 7. B 8. C 5. D 3.
Hướng dẫn giải
Tập hợp các điểm biểu diễn cho số phức z thỏa |z −3 + 4i| = 2 là đường tròn có tâm I(3; −4) và bán
kính bằng R = 2. Suy ra max |z| = IO + R = 7.
Chọn đáp án A
Câu 8. Cho số phức z thỏa mãn |z − 2 − 3i| + |z − 5 + 2i| =
√
34. Gọi M, m lần lượt là giá trị lớn
nhất và giá trị nhỏ nhất của biểu thức |z + 1 + 2i|. Khi đó tổng M + m bằng
A
30
√
34
+
√
34. B
30
√
34
+ 5. C
√
34 + 6. D
30
√
34
+ 6.
Hướng dẫn giải
Liên kết tải về
Tìm thêm: Toán 12

Có thể bạn quan tâm

Xem thêm
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ

Mới nhất trong tuần