Eballsviet.com
Học tập Lớp 12 Toán 12

Bài tập phương pháp lũy thừa giải hệ phương trình Tài liệu ôn tập môn Toán lớp 12

Giới thiệu Tải về Bình luận

Mời quý thầy cô giáo cùng các bạn học sinh lớp 12 cùng tham khảo tài liệu Bài tập phương pháp lũy thừa giải hệ phương trình được Eballsviet.com đăng tải sau đây.

Đây là tài liệu cực kì hữu ích, gồm 19 trang hướng dẫn phương pháp lũy thừa giải hệ phương trình thông qua các bài toán được giải chi tiết. Hy vọng với tài liệu này bạn đọc sẽ “nhớ mặt” được các dạng hệ phương trình có thể sử dụng phương pháp nâng lũy thừa, và hướng sử lý phương trình hệ quả sau đó. Sau đây là nội dung chi tiết, mời các bạn cùng tham khảo và tải tài liệu tại đây.

Bài tập phương pháp lũy thừa giải hệ phương trình

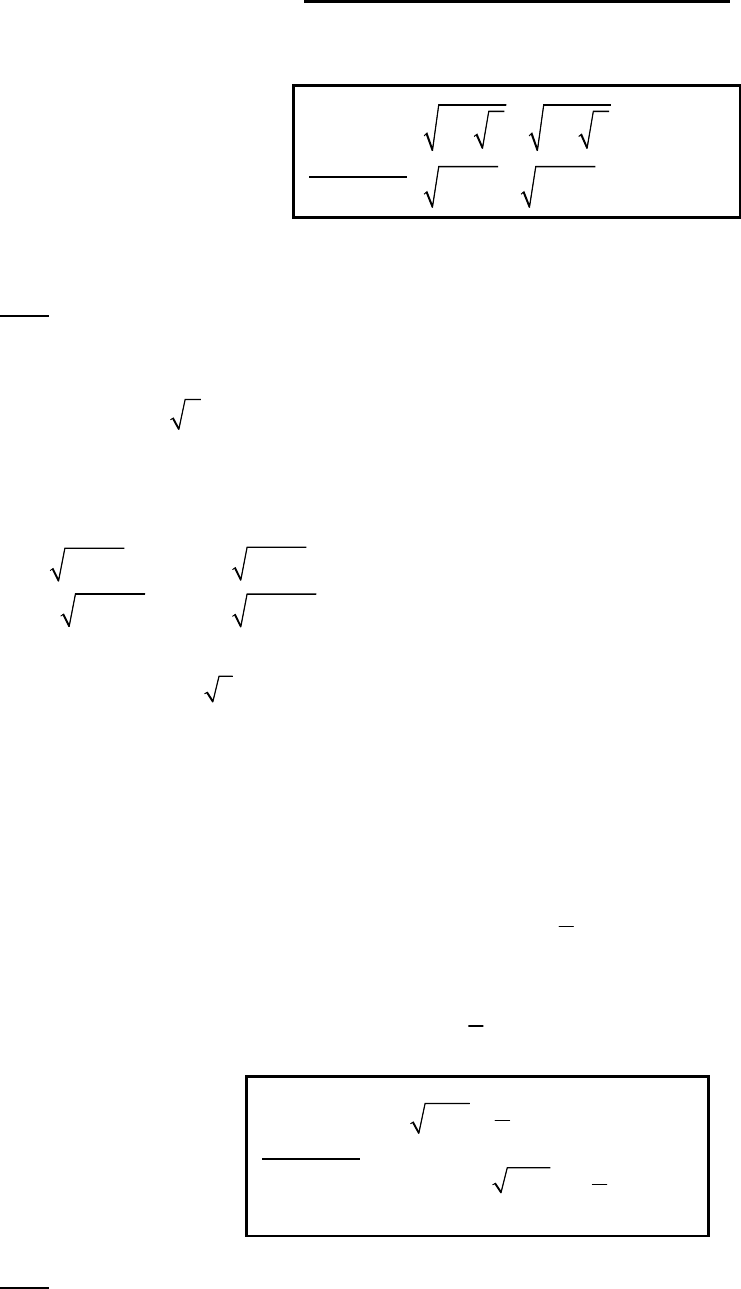
1.PHƯƠNG PHÁP LŨY THỪA
Giải:
Điều kiện :
0
x y
x y
. Nhận xét : Vế trái của phương trình (1) không âm.
Bình phương 2 vế từng phương trình ta được
2
2 4 2
2
8
x x y
x x y
2
4 2 2
2 3
8 4
x y x
x y x
Điều kiện :
x
Phương trình
2 2
3 4 4
x y x x
4 4
y x
Phương trình
4 2 2 4
4 64 16
x y x x
2
4 2 4
4 4 64 16
x x x x
5
32 80 0 6
2
x x y
Vậy nghiệm của hệ phương trình đã cho là
5
;6
2
Giải:
Điều kiện :
1
1
x
y
Bài toán 1.
2 2
2 (1)
4 2
x y x y
x y x y
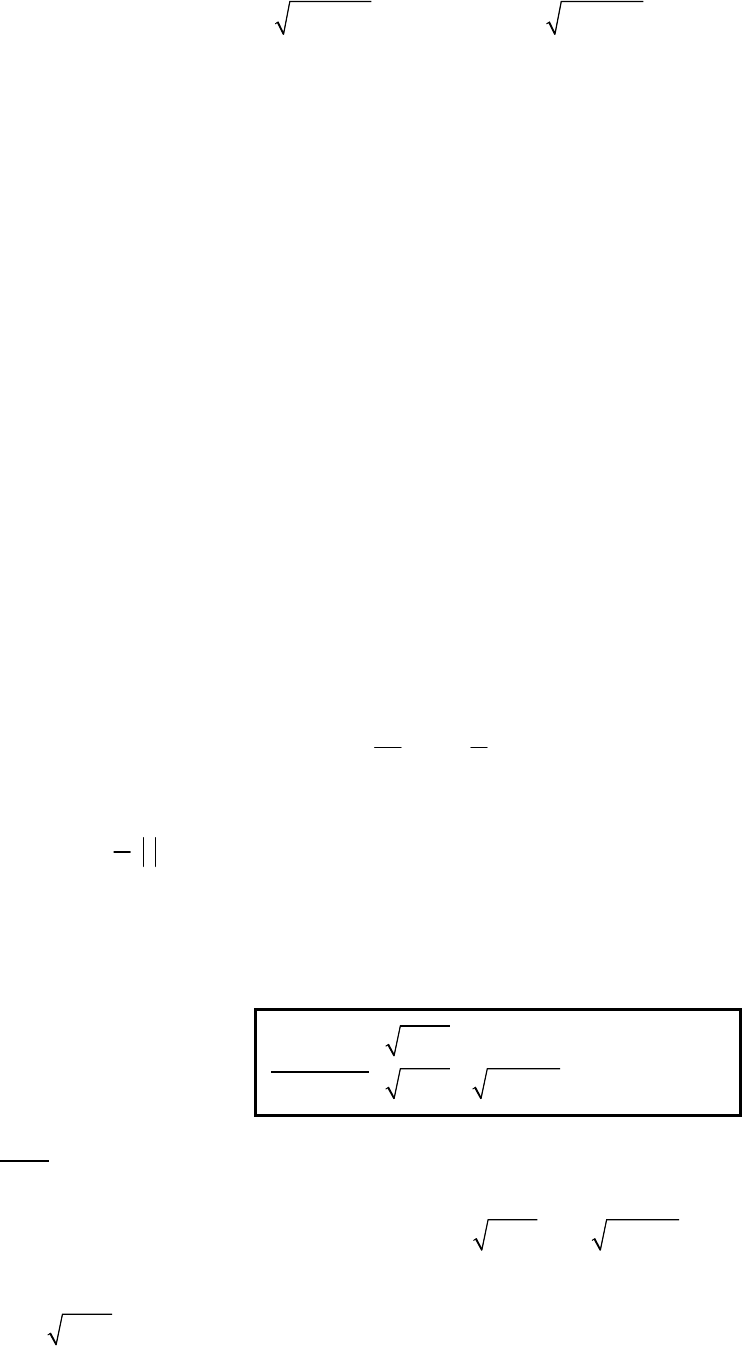
Bài toán 3.
5
1 (1)
2
3
2 3 1 2
4
x y
y x x
Phương trình
2 2
2 2 2 4 4
x x y
2 2
4 2 3
x y x
Điều kiện tương đương :
2
x
. Phương trình
2 2 2
3 4 4 4
x y x x
.
2 2
1 1, 1 4
y x x y x
Thế (4) vào phương trình (3) ta được :
3
2 3 2 2
1 2 1 1 0
y y y y y y
6 5 4 3 2
2 4 2 1 0
y y y y y y
2
4 3 2
1 3 1 0
y y y y y
4 3 2
1 2
3 1 0
y x
y y y y
Xét phương trình :
4 3 2
3 1 0
y y y y
Nếu
0 1
y x
, không thỏa hệ.
Xét
0 :
y
phương trình
2
2
1 1
3 0
y y
y y
 
Đặt
1
, 2.
t y t
y
Phương trình trên trở thành :
2
1 0
t t
, vô nghiệm.
Vậy nghiệm của hệ phương trình đã cho là
1;2
Giải:
Điều kiện :
3 2 0
x y
x y
. Phương trình
2 1 3 2
x y x y
.
2 2 1 3
x y x y
.Điều kiện :
2 1
x y
.
Thế (3) vào phương trình (1) ta được :
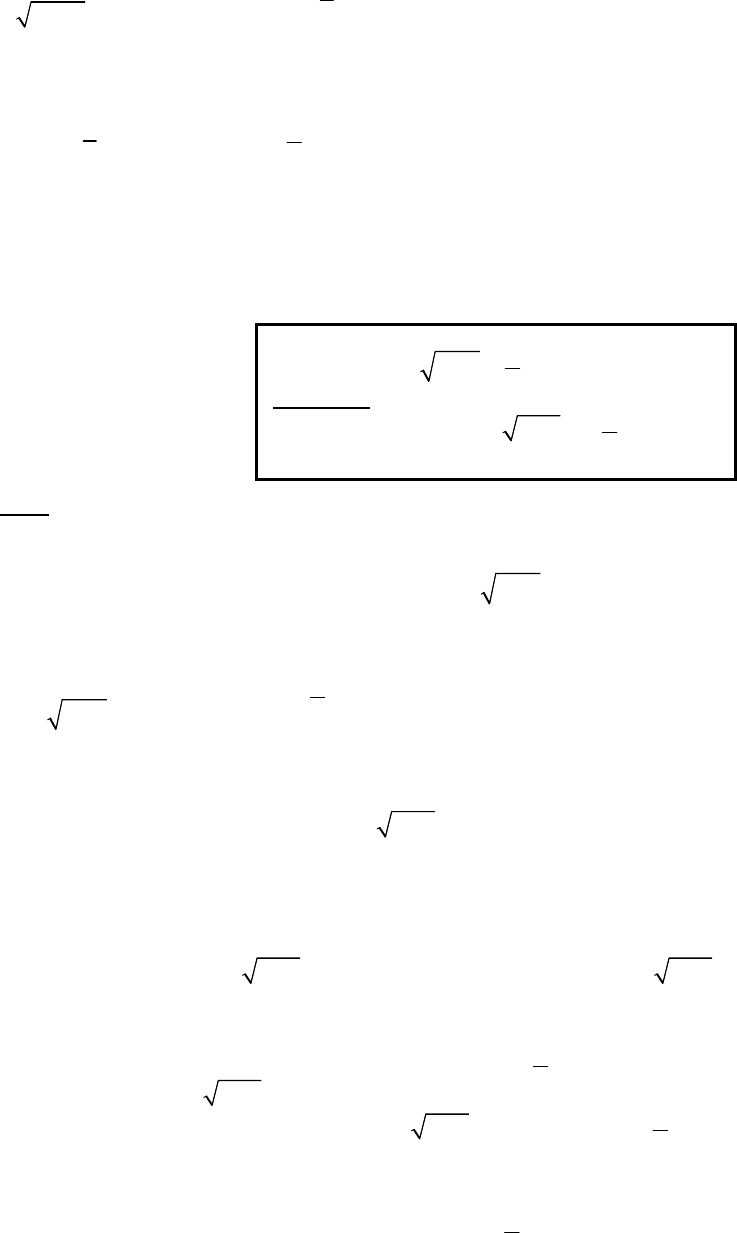
Bài toán 5.
0 (1)
3 2 1 2
x y x y
x y x y
4 1 0 4 1 4
x y y x
Thế (4) vào phương trình (3) ta được :
2 5 1 6 2
x x
2
1
3
5 1 9 6 1
x
x x x
2
1
2
,
3
9
1 3
9 11 2 0
x
x loai
x y
x x
Vậy nghiệm của hệ phương trình đã cho là
1;3
Giải:
Điều kiện :
1
1
y
x
. Phương trình
1 2 2 1 5
x y
.
2 1 2 5
y x
2
5
2
4 1 4 20 25 3
x
y x x
Phương trình
2 4 4 8 3 1 1 4
y x x
Thế (3) vào phương trình (4) ta được :
2
4 20 24 8 3 1 0
x x x x
4 3 2 8 3 1 0
x x x x
4 3 2 2 1 0
x x x
3
3
4
5
2 1 2 , vi x
2
x y
x x loai
Vậy nghiệm của hệ phương trình đã cho là
3
3;
4
Bài toán 6.
5
1 (1)
2
3
2 3 1 2
4
x y
y x x
Liên kết tải về
Tìm thêm: Toán 12

Có thể bạn quan tâm

Xem thêm
Xác thực tài khoản!

Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:

Số điện thoại chưa đúng định dạng!
Số điện thoại này đã được xác thực!
Bạn có thể dùng Sđt này đăng nhập tại đây!
Lỗi gửi SMS, liên hệ Admin
Sắp xếp theo
👨
Đóng
Chỉ thành viên Download Pro tải được nội dung này! Download Pro - Tải nhanh, website không quảng cáo! Tìm hiểu thêm
Mua Download Pro 79.000đ

Mới nhất trong tuần