Tổng hợp đề thi thử Học sinh giỏi Lớp 12 môn Toán năm 2013 30 đề
ĐỀ SỐ 1
(Thời gian: 180 phút)
Câu I: (4 điểm)
Cho hàm số y = x3 + 3x2 - 2 (C)
1/ Khảo sát và vẽ đồ thị.
2/ Giải bất phương trình : 0 ≤ 2006 + 6018x2 - 4012 ≤ 4012.
3/ Viết phương trình tiếp tuyến của đồ thị (C). Biết tiếp tuyến đi qua A(0; -2)
Câu II: (2 điểm)
Tính ![]()
Câu III: (2 điểm)
Giải và biện luận phương trình theo tham số m: |x + 1| + |x - 1| = m
Câu IV: (4 điểm)
Giải các phương trình sau:
1/ Sin(π/2 - πcosx)= cos(3πcosx)
2/ 6x + 4x = 2.9x
Câu V: (2 điểm)
Chứng minh điều kiện cần và đủ để tam giác ABC vuông: Cos2A + Cos2B + Cos2C = 1
Câu VI: (2 điểm): Tính giới hạn sau:![]()
Câu VII: (2 điểm):
Trong hệ Oxy cho hai đường thẳng d1//d2 lần lượt có phương trình là: d1: x - y + 2 = 0; d2: x - y - 2 = 0
1/ Viết phương trình đường thẳng d3 đi qua điểm A(-2; 0) và vuông góc với d2
2/ Viết phương trình đường thẳng d4 sao cho d1, d2, d3, d4 cắt nhau tạo thành một hình vuông.
Câu XIII: (2 điểm)
Chứng minh rằng với a,b> 0 ta có: a5 + b5 ≥ a4b + ab4
ĐỀ SỐ 2
(Thời gian: 180 phút)
Câu 1. (3 điểm)
1. Khảo sát và vẽ đồ thị của hàm số: y = |x|3 - 3|x| - 2 (ξ)
2. Gọi d là đường thẳng đi qua M(2;0) và có hệ số góc k. Tìm k để đường thẳng d cắt (ξ) tại 4 điểm phân biệt.
Câu 2. (4 điểm)
1. Cho dãy số (xn) xác định bởi: 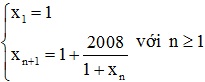
Chứng minh rằng (xn) có giới hạn và tìm giới hạn đó.
2. Tìm m để phương trình: ![]() có nghiệm.
có nghiệm.
Câu 3. (2 điểm)
Cho 1/4 < a, b, c, d < 1. Tìm giá trị nhỏ nhất của biểu thức:
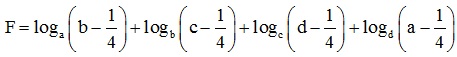
Câu 4. (3 điểm)
1. Giải phương trình: ![]()
2. Tìm nghiệm của phương trình ![]() thỏa mãn: 2008 < x < 2009
thỏa mãn: 2008 < x < 2009
Câu 5. (2 điểm)
Cho tam giác ABC biết A(1; -2), hai đường phân giác trong của góc B và C lần lượt có phương trình là: (d1): 3x + y - 3 = 0 và (d2): x - y - 1 = 0. Lập phương trình các cạnh của tam giác ABC.
Câu 6. (4 điểm)
Cho một tam diện vuông Oxyz và một điểm A cố định bên trong tam diện. Gọi khoảng cách từ A đến ba mặt phẳng Oyz, Ozx, Oxy lần lượt là a, b, c. Một mặt phẳng (α) qua A cắt Ox, Oy, Oz lần lượt tại M, N, P.
1. Chứng minh rằng: ![]()
2. Xác định vị trí của mặt phẳng (α) để thể tích của tứ diện OMNP đạt giá trị nhỏ nhất. Khi thể tích tứ diện OMNP nhỏ nhất, hãy chỉ rõ vị trí điểm A.
3. Chứng minh rằng: (MN + NP + PM)2 ≤ 6(OM2 + ON2 + OP2)
Câu 7. (2 điểm)
Cho 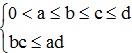 . Chứng minh rằng: ab.bc.cd.da ≥ ad.dc.cb.ba
. Chứng minh rằng: ab.bc.cd.da ≥ ad.dc.cb.ba
Download tài liệu để xem chi tiết.
Chọn file cần tải:
Theo Nghị định 147/2024/ND-CP, bạn cần xác thực tài khoản trước khi sử dụng tính năng này. Chúng tôi sẽ gửi mã xác thực qua SMS hoặc Zalo tới số điện thoại mà bạn nhập dưới đây:
Chủ đề liên quan
Có thể bạn quan tâm
-

Văn mẫu lớp 11: Phân tích hai câu đầu của bài thơ Chiều tối (2 Dàn ý + 9 mẫu)
-

Liên hệ bản thân trong nghị luận xã hội
-

Viết đoạn văn cảm nhận về bài thơ Bữa cơm quê của Đoàn văn Cừ
-

Điều chỉnh nội dung môn Ngữ văn năm 2025 cấp THCS
-

Văn mẫu lớp 10: Nghị luận về vấn đề nhìn nhận và sửa chữa sai lầm (Dàn ý + 8 Mẫu)
-
Bài tập trắc nghiệm môn Toán lớp 9
-

Đề cương ôn tập học kì 2 môn Công nghệ 6 năm 2024 - 2025 (Sách mới)
-

Tả lại quang cảnh buổi trình diễn văn nghệ ở trường em
-

Đề thi học kì 2 môn Tin học 5 năm 2024 - 2025 sách Rô bốt thông minh
-

Đề cương ôn thi học kì 2 môn Tin học 7 năm 2024 - 2025 (Sách mới)
Mới nhất trong tuần
-

Đề thi thử THPT Quốc gia năm 2025 môn Ngữ văn trường THPT Yên Dũng 2, Bắc Giang
100+ -

Các dạng bài tập cực trị của hàm số
50.000+ -

Tóm tắt lý thuyết và giải nhanh Toán 12
50.000+ 1 -

Các dạng bài tập tính đơn điệu của hàm số
50.000+ -
524 câu hỏi vận dụng cao trong các đề thi THPT Quốc gia
5.000+ -

Bộ đề thi chọn học sinh giỏi môn Toán lớp 12
10.000+ -

Bộ đề thi khảo sát chất lượng đầu năm môn Toán lớp 12 năm 2023 - 2024
10.000+ -
Lý thuyết và bài tập trắc nghiệm số phức
100+ -

Hướng dẫn giải các dạng toán tiệm cận của đồ thị hàm số
1.000+ -

Bài tập trắc nghiệm ứng dụng đạo hàm để khảo sát và vẽ đồ thị hàm số
1.000+






 Đề thi học kì 1 Lớp 12
Đề thi học kì 1 Lớp 12
 Đề thi giữa học kì 1 Lớp 12
Đề thi giữa học kì 1 Lớp 12
 Đề thi giữa học kì 2 Lớp 12
Đề thi giữa học kì 2 Lớp 12
 Đề thi học kì 2 Lớp 12
Đề thi học kì 2 Lớp 12
 Soạn Văn 12 KNTT
Soạn Văn 12 KNTT
 Soạn Văn 12 CTST
Soạn Văn 12 CTST
 Soạn Văn 12 Cánh Diều
Soạn Văn 12 Cánh Diều
 Văn 12
Văn 12
 Toán 12 Chân trời sáng tạo
Toán 12 Chân trời sáng tạo