Đề thi thử Đại học năm 2013 - môn Toán (Đề 24) Đề thì môn Toán số 24

ĐỀ THI THỬ ĐẠI HỌC - CAO ĐẲNG
NĂM 2012 - 2013

MÔN THI: TOÁN

Đề số 04

PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm):

Câu I (2 điểm) Cho hàm số y = f(x) = mx³ + 3mx² - (m - 1)x - 1, m là tham số

1. Khảo sát sự biến thiên và vẽ đồ thị của hàm số trên khi m = 1.

2. Xác định các giá trị của m để hàm số y = f(x) không có cực trị.

Câu II (2 điểm): Giải phương trình:

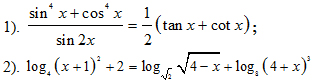
Câu III (1 điểm) Tính tích phân: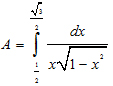

Câu IV (1 điểm) Cho hình nón có đỉnh S, đáy là đường tròn tâm O, SA và SB là hai đường sinh, biết SO = 3, khoảng cách từ O đến mặt phẳng SAB bằng 1, diện tích tam giác SAB bằng 18. Tính thể tích và diện tích xung quanh của hình nón đã cho.

Câu V (1 điểm) Tìm m để hệ bất phương trình sau có nghiệm:

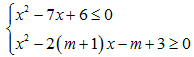
B. PHẦN RIÊNG (3 điểm): Thí sinh chỉ làm một trong hai phần (Phần 1 hoặc phần 2)

1. Theo chương trình chuẩn.

Câu VI.a (2 điểm)

1. Cho tam giác ABC biết các cạnh AB, BC lần lượt là 4x + 3y – 4 = 0; x – y – 1 = 0. Phân giác trong của góc A nằm trên đường thẳng x + 2y – 6 = 0. Tìm tọa độ các đỉnh của tam giác ABC.

2. Cho hai mặt phẳng (P): x + 2y - 2z + 5 = 0; (Q): x + 2y - 2z = 0. Viết phương trình của mặt cầu (S) đi qua gốc tọa độ O, qua điểm A(5;2;1) và tiếp xúc với cả hai mặt phẳng (P) và (Q).

Câu VII.a (1 điểm) Tìm số nguyên dương n thỏa mãn các điều kiện sau:

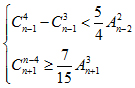
(Ở đây A^k_n, C^k_n lần lượt là số chỉnh hợp và số tổ hợp chập k của n phần tử)

2. Theo chương trình nâng cao.

Câu VI.b (2 điểm)

1. Cho đường thẳng d: x – 5y – 2 = 0 và đường tròn (C): x2 + y2 + 2x - 4y - 8 = 0. Xác định tọa độ các giao điểm A, B của đường tròn (C) và đường thẳng d (điểm A có hoành độ dương). Tìm tọa độ C thuộc đường tròn (C) sao cho tam giác ABC vuông ở B.

2. Cho mặt phẳng (P): x- 2y - 2z - 1 = 0 và các đường thẳng: 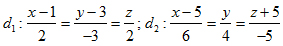. Tìm các điểm M thuộc d₁, N thuộc d₂ sao cho MN // (P) và cách (P) một khoảng bằng 2.

Câu VII.b: Tính đạo hàm f’(x) của hàm số 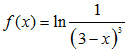và giải bất phương trình: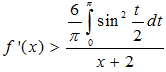

Download tài liệu để xem thêm chi tiết