Đề thi thử đại học môn Toán năm 2014 tỉnh Bắc Giang Có đáp án

I. PHẦN CHUNG CHO TẤT CẢ CÁC THÍ SINH (7 điểm)

Câu 1 (2 điểm):

Cho hàm số y = 2x³ - 3(2m + 1)x² + 6m(m + 1)x + 1 có đồ thị (1)

a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số (1) khi m = 0.

b. Tìm m để đồ thị hàm số (1) đồng biến trên khoảng (2; +∞).

Câu 2 (1 điểm) Giải phương trình sau:

Câu 3 (1 điểm) Giải phương trình sau:

Câu 4 (1 điểm) Tìm m để hệ phương trình sau có 3 cặp nghiệm thực phân biệt:

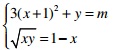
Câu 5 (1 điểm)

Cho hình chóp tứ giác S.ABCD có đáy là hình chữ nhật, SA vuông góc với đáy, G là trọng tâm tam giác SAC, mặt phẳng (ABG) cắt SC tại M, cắt SD tại N. Tính thể tích của khối đa diện MNABCD biết SA = SB = a và góc hợp bởi đường thẳng AN và mặt phẳng (ABCD) bằng 30^o.

Câu 6 (1 điểm)

Cho x, y, z thỏa mãn là các số thực: x² - xy + y² = 1. Tìm giá trị lớn nhất và giá trị nhỏ nhất của biểu thức:

II. PHẦN RIÊNG (3 điểm): Thí sinh chỉ được làm một trong hai phần (Phần A hoặc phần B)

A. Theo chương trình chuẩn.

Câu 7a (1 điểm): Trong mặt phẳng Oxy, cho tam giác ABC với AB = √5, C(-1; -1), đường thẳng AB có phương trình: x + 2y - 3 = 0 và trọng tâm tam giác ABC thuộc đường thẳng d: x + y - 2 = 0. Tìm tọa độ đỉnh A và B.

Câu 8a (1 điểm): Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn (C): x² + y² - 4x - 4y + 4 = 0 và đường thẳng d có phương trình: x + y - 2 = 0. Chứng minh rằng d luôn cắt (C) tại hai điểm phân biệt A và B. Tìm tọa độ điểm M trên đường tròn (C) sao cho diện tích tam giác MAB lớn nhất.

Câu 9a (1 điểm): Cho khai triển:

. Tính a₄.

B. Theo chương trình nâng cao

Câu 7b (1 điểm): Trong mặt phẳng Oxy, cho tam giác ABC biết B(2; -1), đường cao và đường phân giác trong qua đỉnh A và C lần lượt có phương trình: 3x - 4y + 27 = 0 và x + 2y - 5 = 0. Viết phương trình các cạnh của tam giác ABC.

Câu 8b (1 điểm): Trong mặt phẳng Oxy, viết phương trình chính tắc của Elip (E), biết rằng tâm sai của E bằng và hình chữ nhật cơ sở có diện tích bằng 24.

Câu 9b (1 điểm): Một hộp đựng 15 viên bi, trong đó có 7 viên bi xanh và 8 viên bi đỏ. Lấy ngẫu nhiên 3 viên bi (không kể thứ tự ra khỏi hộp). Tính xác xuất để trong 3 viên bi lấy ra có ít nhất 1 viên bi đỏ.

Download tài liệu để xem chi tiết.